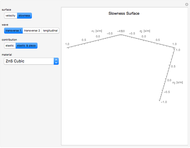
Impedance Spectra of Piezoelectric Rods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
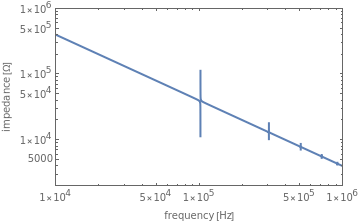
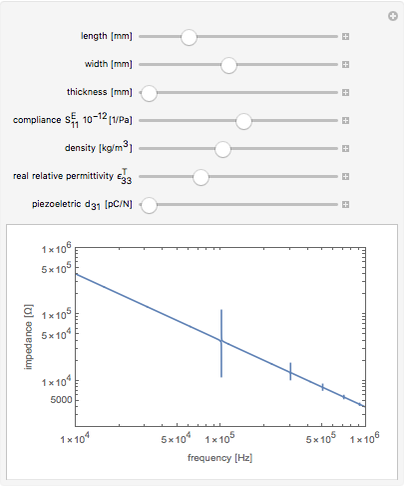
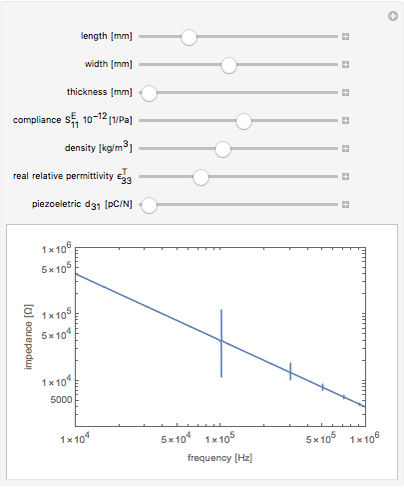
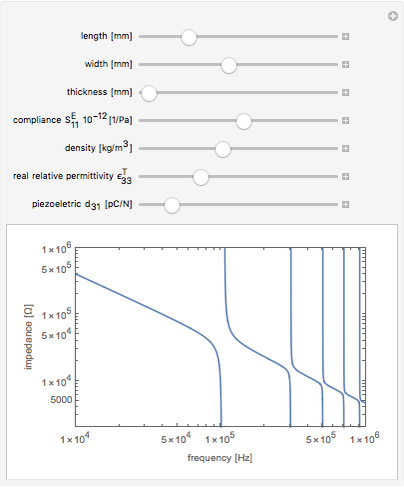
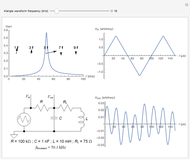
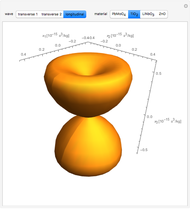
This Demonstration calculates the impedance spectrum of a piezoelectric rod. The default values are for the common piezoelectric material lithium niobate. Spikes in the spectrum indicate the locations of resonances. The frequency where the impedance is at a minimum is considered a resonance, and the frequency where a maximum occurs is considered an anti-resonance. The lowest frequency spike is the fundamental resonance, and the higher spikes are the harmonics that occur at odd multiples of the fundamental.
Contributed by: Robert McIntosh (March 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the converse piezoelectric effect (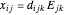 ), an applied electric field (
), an applied electric field (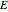 ) causes an induced strain (
) causes an induced strain ( ) in the material [1]. This Demonstration predicts the resonance frequencies of the sample based on its dimensions and material coefficients.
) in the material [1]. This Demonstration predicts the resonance frequencies of the sample based on its dimensions and material coefficients.
The impedance can be calculated using the following formulas [2]:
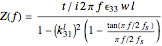
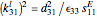 .
.
This equation is only valid assuming four conditions:
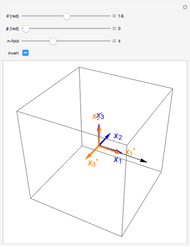
1. The electric field is applied in the thickness ( ) direction.
) direction.
2. 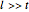
3. 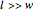
4. 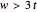
The formula for  gives the low-frequency length-extensional modes of bar samples. Bar samples are parallelepipeds that have one dimension significantly longer than the others. For length-extensional modes, the bar’s primary vibration direction is along its longest dimension.
gives the low-frequency length-extensional modes of bar samples. Bar samples are parallelepipeds that have one dimension significantly longer than the others. For length-extensional modes, the bar’s primary vibration direction is along its longest dimension.
Increasing the length dimension of the rod results in lower resonant frequencies because the sample becomes clamped and cannot respond as quickly to the applied electric field.
Move the sliders to observe which parameters have the largest influence on the resonance locations.
References
[1] R. E. Newnham, Properties of Materials, New York: Oxford University Press, 2005.
[2] IEEE, IEEE Standard on Piezoelectricity, ANSI/IEEE Std 176-1987, 1988. doi.10.1109/IEEESTD.1988.79638.
Permanent Citation