Semi-Annular Spiral Billiard with Periodic Orbits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
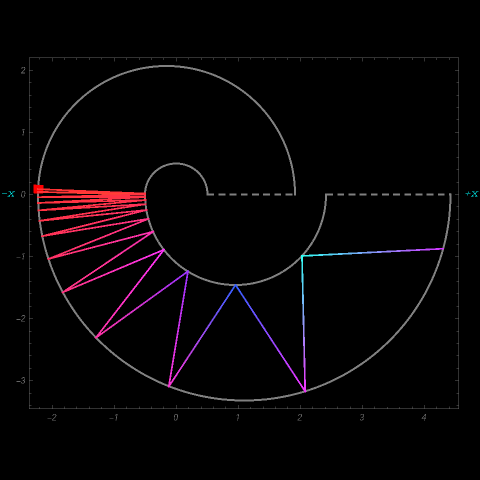
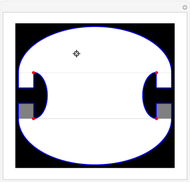
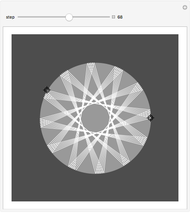
This Demonstration shows spiral-shaped billiard tables patched together using annular pieces. Starting at zero radians on the positive  axis, and repeating every
axis, and repeating every  radians counter-clockwise around the spiral, periodic orbits occur where tangents to a table's inner and outer curved boundaries are parallel for the same spiral angle. To construct a table, users can choose the number of loops around the spiral and the rate at which the width of the spiral increases.
radians counter-clockwise around the spiral, periodic orbits occur where tangents to a table's inner and outer curved boundaries are parallel for the same spiral angle. To construct a table, users can choose the number of loops around the spiral and the rate at which the width of the spiral increases.
Contributed by: William C. Hill (March 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The trajectory calculations are based on figure 1 on page 539 of [1].
Reference
[1] J. S. Espinoza Ortiz and R. Egydio de Carvalho, "Energy Spectrum and Eigenfunctions through the Quantum Section Method," Brazilian Journal of Physics, 31(4), 2001 pp. 538–545.
Permanent Citation