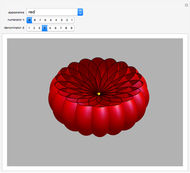
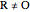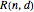Special Rose Surfaces

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
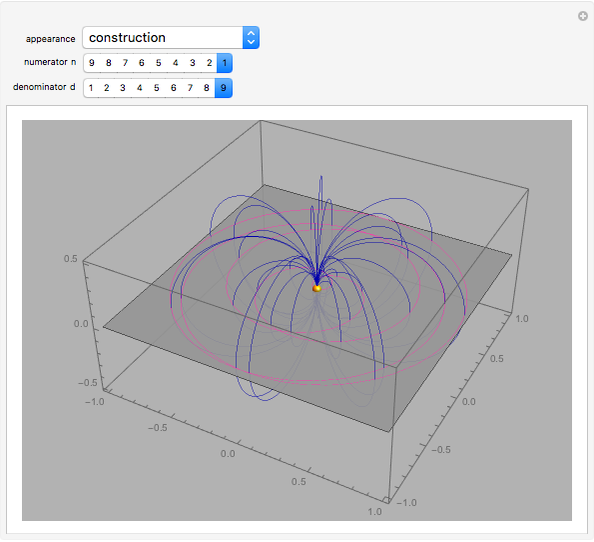
In the plane 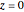 , a rose (or rhodonea) is a curve
, a rose (or rhodonea) is a curve 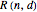 , given by the polar equation
, given by the polar equation 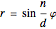 , where
, where 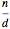 is a positive rational number in lowest terms. This is a directing curve of a special rose surface
is a positive rational number in lowest terms. This is a directing curve of a special rose surface  presented in this Demonstration.
presented in this Demonstration.
Contributed by: Sonja Gorjanc (University of Zagreb) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
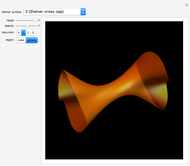
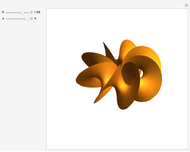
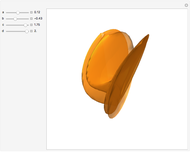
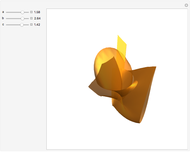
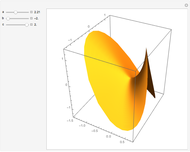
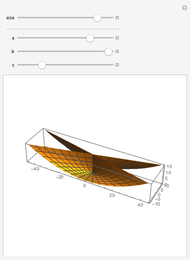
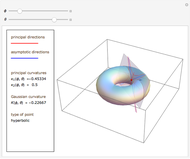
This Demonstration shows the parts of special rose surfaces 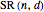 , where
, where 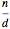 is the simplest form of the rational number that you choose using the setter. For every choice of
is the simplest form of the rational number that you choose using the setter. For every choice of 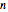 and
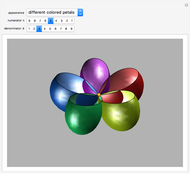
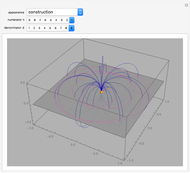
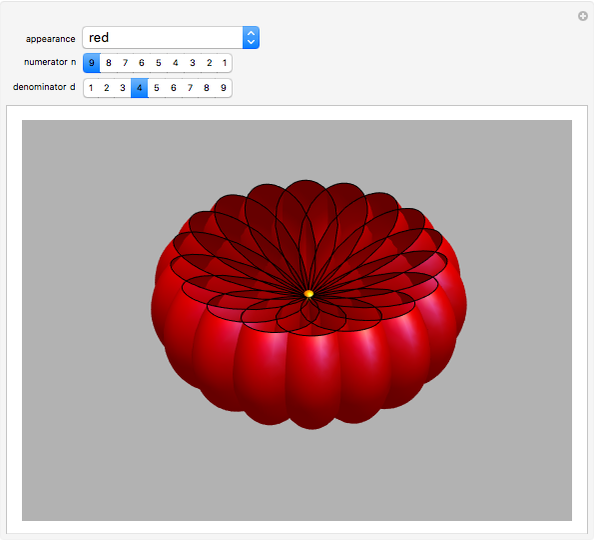
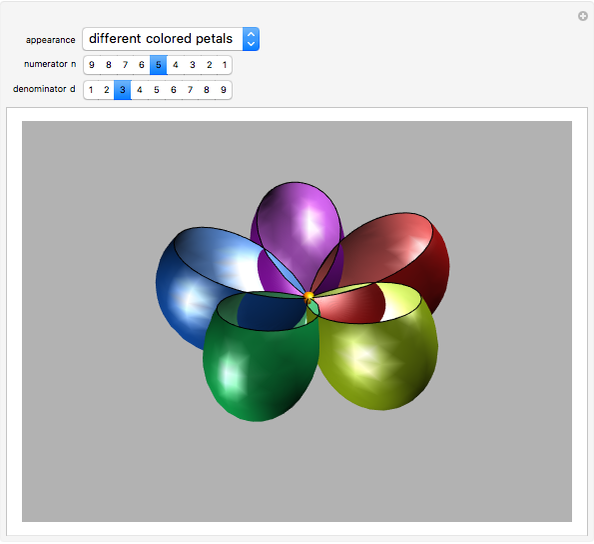
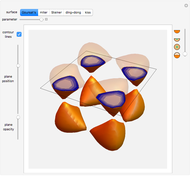
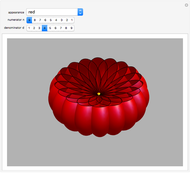
and  there are three possibilities for surface presentation: red colored surface (Snapshot 1), petals of surface colored by different colors (Snapshot 2), and the illustration of surface construction as the system of circles (Snapshot 3).
there are three possibilities for surface presentation: red colored surface (Snapshot 1), petals of surface colored by different colors (Snapshot 2), and the illustration of surface construction as the system of circles (Snapshot 3).
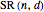 is an algebraic surface with the following properties:
is an algebraic surface with the following properties:
• If 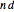 is odd and
is odd and 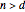 , the order of
, the order of 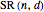 is
is 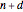 ,
,  is an
is an  -fold point,
-fold point,  is an
is an 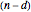 -fold line, and there are
-fold line, and there are  petals.
petals.
• If 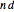 is even and
is even and 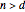 , the order of
, the order of 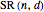 is
is 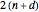 ,
, 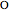 is
is 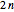 -fold point,
-fold point,  is a
is a 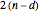 -fold line, and and there are
-fold line, and and there are 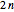 petals.
petals.
• If 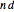 is odd and
is odd and 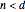 , the order of
, the order of 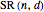 is
is 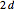 ,
, 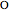 is a
is a  -fold point, and there are
-fold point, and there are  petals.
petals.
• If 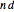 is even and
is even and 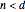 , the order of
, the order of 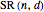 is
is 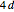 ,
, 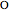 is a
is a 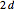 -fold point, and there are
-fold point, and there are 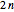 petals.
petals.
Based on work by the author in "Rose Surfaces and Their Visualizations," submitted to J. Geom. Graph.
Reference:
G. Loria, Spezielle Algebraische und Transzendente Ebene Kurven, Leipzig-Berlin: B. G. Teubner, 1910.
Permanent Citation