Pedal Curves of Conics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
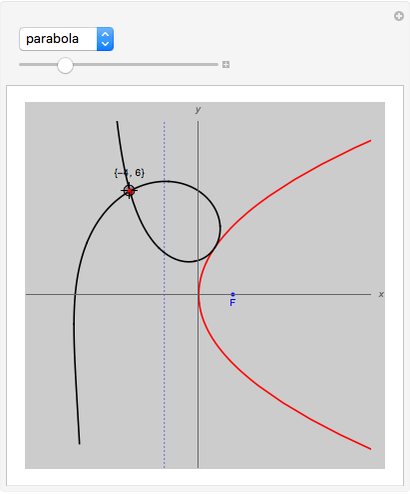
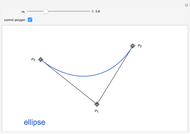
The pedal curve 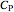 of a curve
of a curve 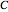 with respect to a point
with respect to a point 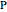 (the pedal point) is the locus of the foot of the perpendicular from
(the pedal point) is the locus of the foot of the perpendicular from 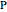 to the tangent line of the curve
to the tangent line of the curve 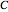 .
.
Contributed by: Sonja Gorjanc (September 2012)
GEFFA Summer School 2012 - Rijeka
Open content licensed under CC BY-NC-SA
Snapshots
Details
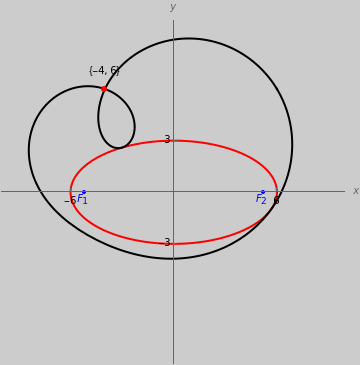
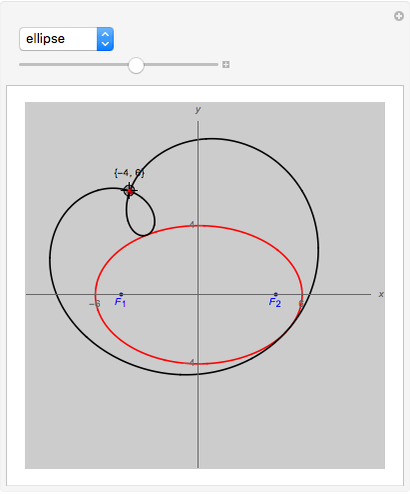
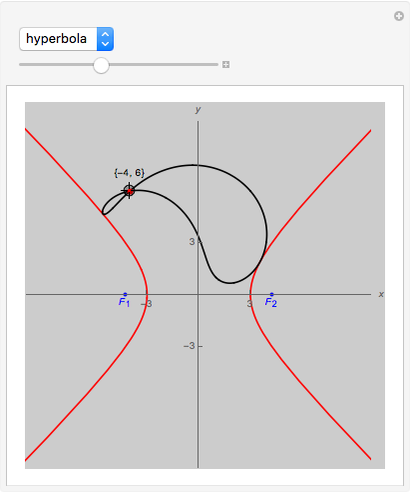
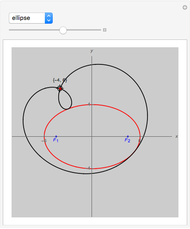
Generally, the pedal curve of a conic is a bicircular quartic (a fourth-order curve with double absolute points) with a real double point at the pedal point 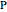 . The point
. The point 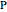 is a node, a cusp, or an isolated double point depending on whether it is outside, on, or inside the conic
is a node, a cusp, or an isolated double point depending on whether it is outside, on, or inside the conic 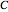 , respectively.
, respectively.
In special cases, this quartic splits into a pair of lines and a curve of the lower order.
• If 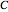 is a parabola,
is a parabola, 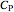 splits into the line at infinity and a circular cubic.
splits into the line at infinity and a circular cubic.
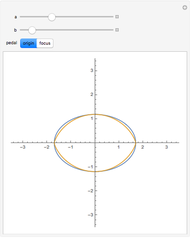
• If 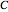 is an ellipse or a hyperbola and
is an ellipse or a hyperbola and 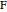 is one of its foci,
is one of its foci,  is a circle. More precisely, the pedal curve splits into the pair of isotropic lines through
is a circle. More precisely, the pedal curve splits into the pair of isotropic lines through 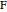 and a circle.
and a circle.
• If 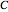 is a parabola and
is a parabola and 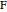 is its focus,
is its focus,  is a line. More precisely, the pedal curve splits into the line at infinity, the pair of isotropic lines through
is a line. More precisely, the pedal curve splits into the line at infinity, the pair of isotropic lines through 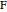 , and the tangent line to the parabola at its vertex.
, and the tangent line to the parabola at its vertex.
References
[1] A. Gray, Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed., Boca Raton: CRC Press LLC, 1998.
[2] G. Salmon, A Treatise on the Higher Plane Curves, New York: Chelsea Publishing Company (reprint), 1960.
Permanent Citation