State of Light Polarization
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
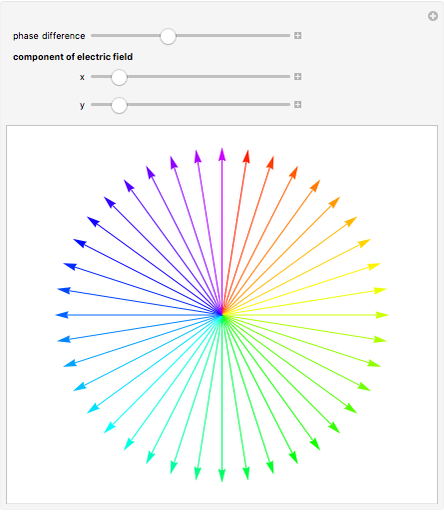
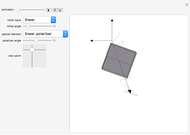
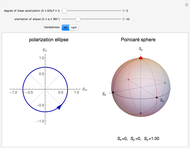
This Demonstration allows you to visualize elliptical, linear, or circular state of light polarization. For a transverse electromagnetic wave propagating in the 
direction, any polarization state can be expressed in terms of linear polarizations along the 
and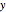 
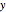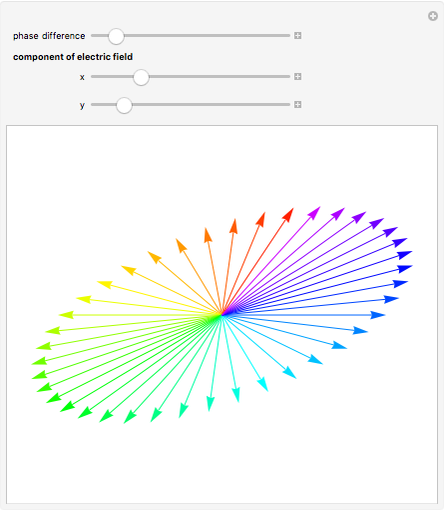
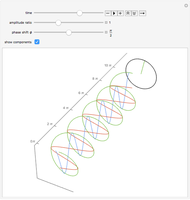
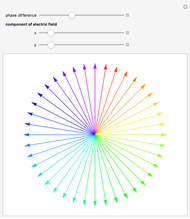
directions, which are transverse to the direction of propagation. To visualize a state of polarization, vary the or components of the electric field (i.e., polarization), and/or the phase difference between the two—that is, the phase of the component relative to the 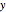component. The direction of electric field rotation (for elliptical and circular polarization) is coded using the visible part of the electromagnetic spectrum: red → yellow → green → blue → violet.
Contributed by: Ertan Salik (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
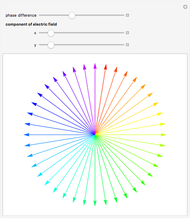
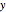Snapshot 1: For the very special cases of 90- and 270-degree phase differences with equal and components, you get circularly polarized light.
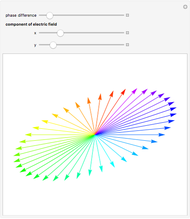
Snapshot 2: If the phase difference is nonzero, then in general you get elliptical polarization. Positive phase difference means that the component leads the 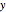component. For example, if the component leads the 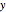component by 0–180 degrees, and if the beam is propagating toward the observer, the observer will see it rotating counterclockwise. For a phase difference between 180–360 degrees, however, the observer will see it rotating clockwise. Follow the arrows: red → yellow → green → blue → violet.
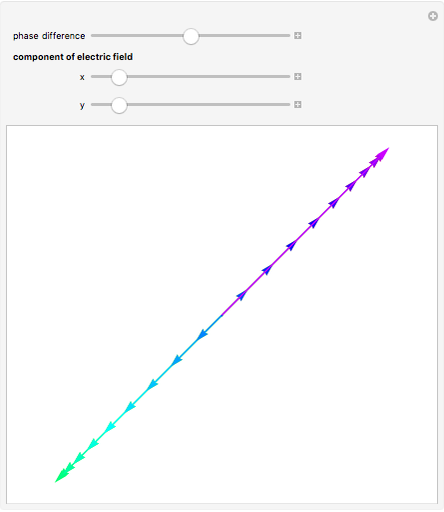
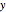Snapshot 3: If the phase difference is 0, you get linear polarization, the direction of which is determined by the magnitudes of the and components.
Permanent Citation
Polarization State Generator
Siva Perla
Light Beams through Multiple Polarizers
S. M. Blinder
Variable States of Polarization Incident on a Wave Plate
Randall J. Hinton (Temple University)
Understanding Polarization with an Analogy
Enrique Zeleny
A Rotating Waveplate Polarization Analyzer
Beth Schaefer and Edward Collett
Polarization of an Optical Wave through Polarizers and Wave Plates
Fred E. Moolekamp and Kevin L. Stokes (University of New Orleans)
Radially Polarized Laser Beam Intensity Distributions
Yousef I. Salamin
Light Polarization and Stokes Parameters
Gianni Di Domenico and Antoine Weis
Circular and Elliptic Polarization of Light Waves
Jochen Autschbach
Light Refraction with a Waterdrop
Donald Barnhart, developer of Rayica and LensLab
