System of Pendulums: A Realization of the Sine-Gordon Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
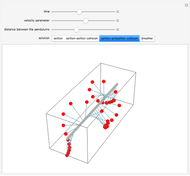
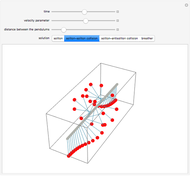
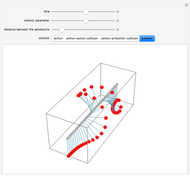
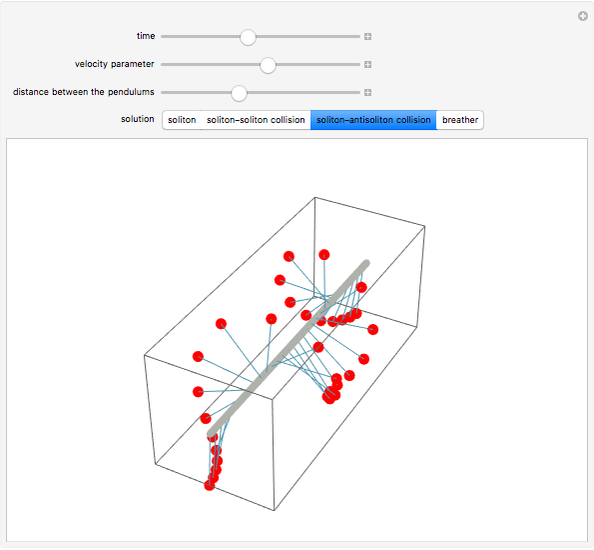
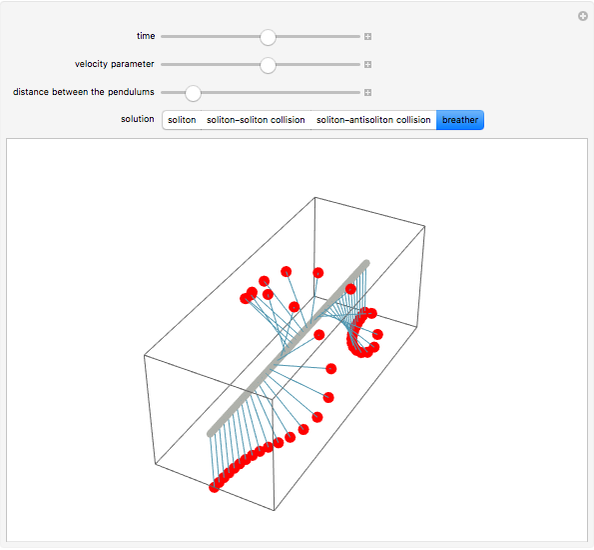
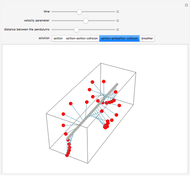
A row of pendulums hang from a rod and are coupled by torsion springs. This system can be described by a nonlinear differential equation called the sine-Gordon equation. The solutions can exhibit different types of behavior, involving solitons, antisolitons, and their interactions.
Contributed by: Balázs Meszéna (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The sine-Gordon equation has the form  . It is a nonlinear PDE that is exactly solvable. A realization of the model is a system of coupled pendulums. Here,
. It is a nonlinear PDE that is exactly solvable. A realization of the model is a system of coupled pendulums. Here, 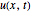 is the angle of a pendulum with coordinate
is the angle of a pendulum with coordinate  at time
at time  .
.
The first type of solution we can see is the soliton:
 .
.
Moving at velocity  , the soliton preserves its shape during the pendulum motion. There are actually two types of soliton: the left-handed soliton ("kink"), and the right-handed anti-soliton ("antikink"). Due to the relativistic covariance of the equation, the solution has an interesting feature, namely that the size of the soliton decreases as the soliton moves faster, suggestive of the Lorentz contraction.
, the soliton preserves its shape during the pendulum motion. There are actually two types of soliton: the left-handed soliton ("kink"), and the right-handed anti-soliton ("antikink"). Due to the relativistic covariance of the equation, the solution has an interesting feature, namely that the size of the soliton decreases as the soliton moves faster, suggestive of the Lorentz contraction.
Other types of solutions can be characterized as soliton-soliton:
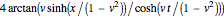 ,
,
and as soliton-antisoliton collisions:
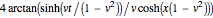 .
.
In these cases, two solitons (or a soliton and an anti-soliton) move from the ends of the box with velocities 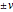 and collide with each other.
and collide with each other.
The last type of solution is the so-called breather:
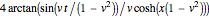 ,
,
which is localized and periodic. It can be gotten from the soliton-antisoliton solution by the substitution 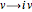 .
.
Permanent Citation