Chaotic Dynamics of a Magnetic Pendulum

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
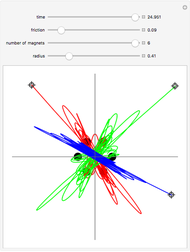
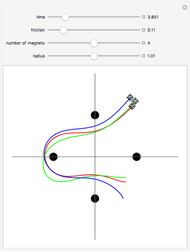
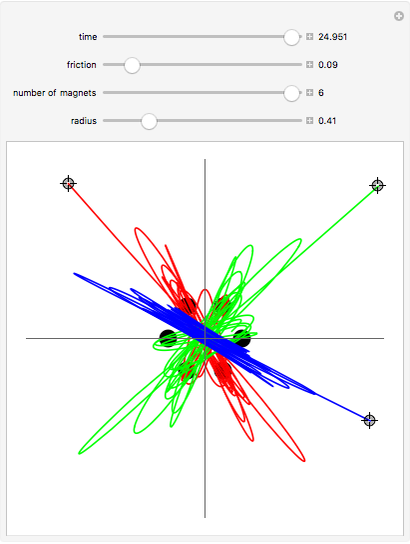
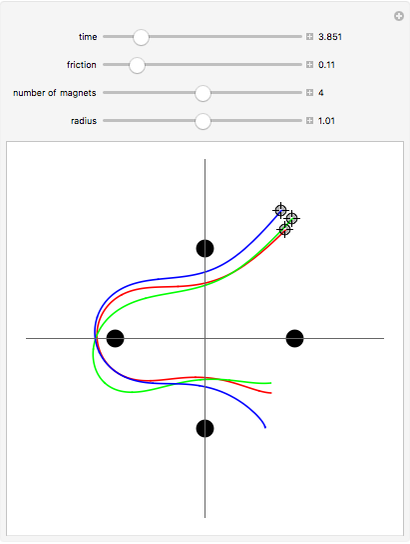
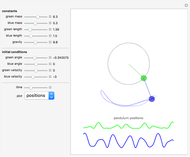
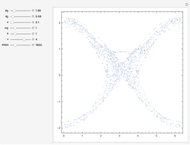
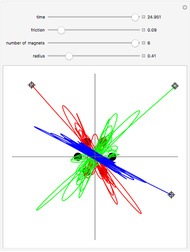
A highly sensitive dependence on initial conditions is one of the fundamental properties of chaos. An example of such a chaotic system is a magnetic pendulum in which a magnet attached to the end of a pendulum oscillates over a plane where a set of attractive magnets are present. Depending on the initial conditions, the pendulum will come to rest at one of the magnet positions, but the final resting point can be highly sensitive to initial conditions. The trajectory generated from of each of the three initial positions is shown using a parametric plot. By varying the initial position, friction of the system, and magnet position, the final state of each trajectory can be altered.
Contributed by: Galen Craven (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] H. Peitgen, H. Jurgens, and D. Saupe, Chaos and Fractals: New Frontiers of Science, New York: Springer-Verlag, 2004.
Permanent Citation
"Chaotic Dynamics of a Magnetic Pendulum"
http://demonstrations.wolfram.com/ChaoticDynamicsOfAMagneticPendulum/
Wolfram Demonstrations Project
Published: March 7 2011