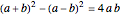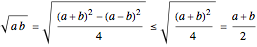Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Arithmetic-Geometric Mean Inequality (I)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

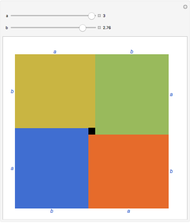
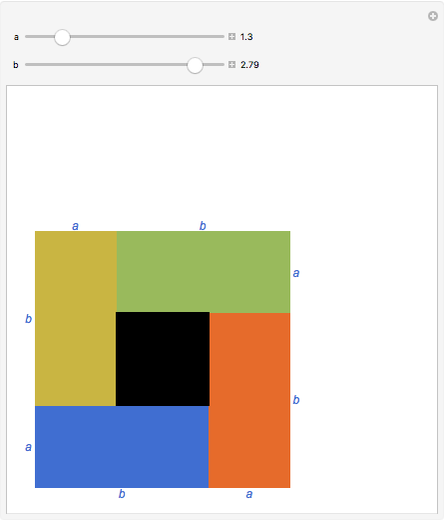
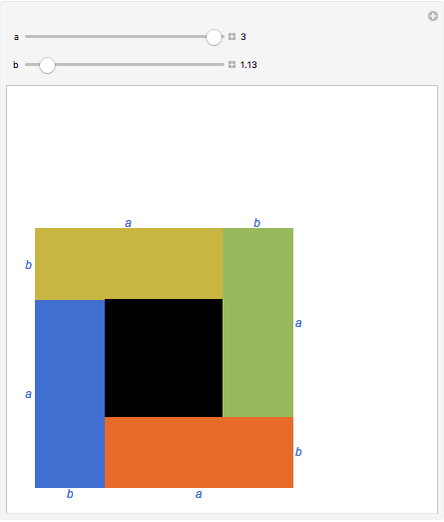
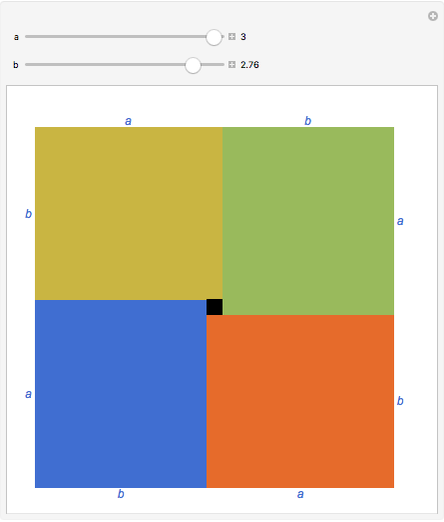
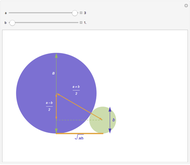
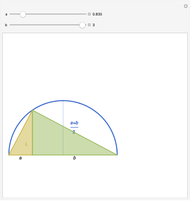
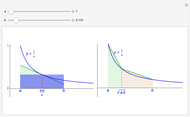
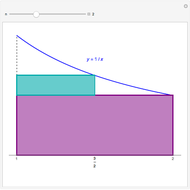
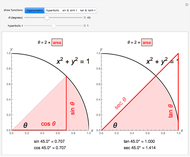
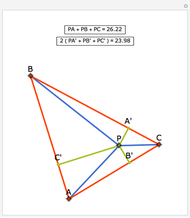
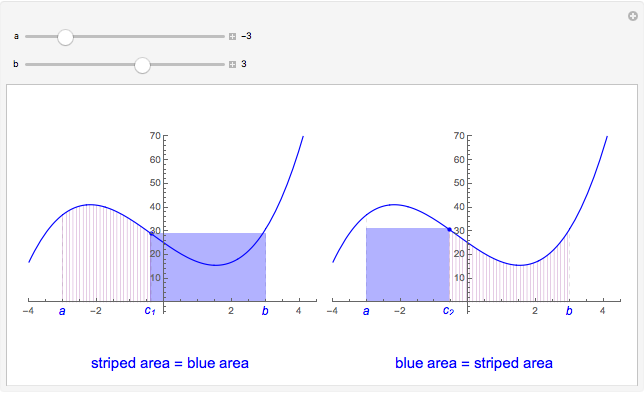
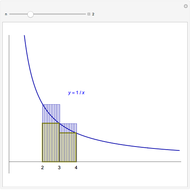
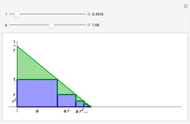
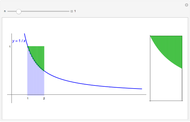
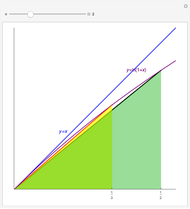
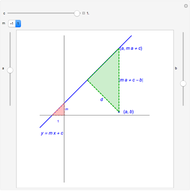
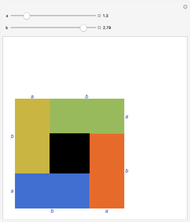
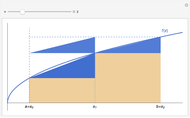
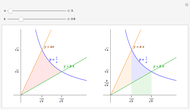
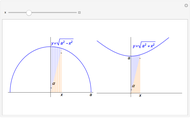
The arithmetic-geometric mean inequality: 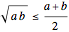, for .

[more]

The figure shows that , therefore .

[less]

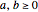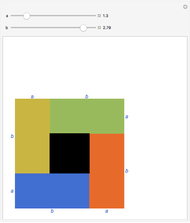
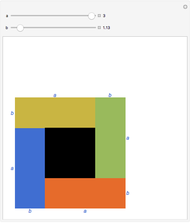
Contributed by: Soledad Mª Sáez Martínez and Félix Martínez de la Rosa (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

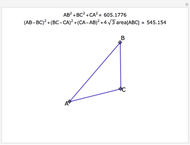
Reference: D. Schattschneider, "Proof without Words: The Arithmetic Mean-Geometric Mean Inequality," Mathematics Magazine, 59(1), 1986 p. 11.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send