Flett's Theorem

Initializing live version

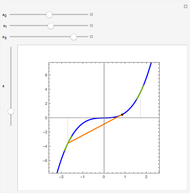
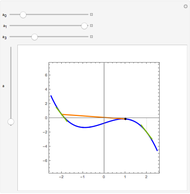
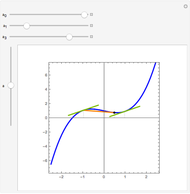
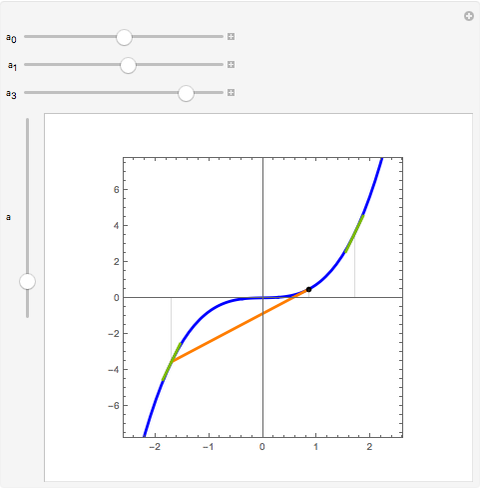
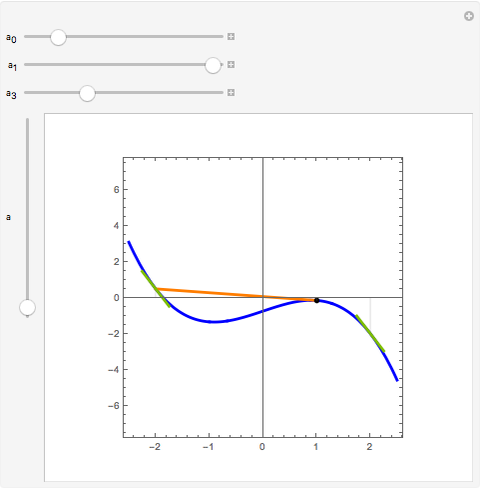
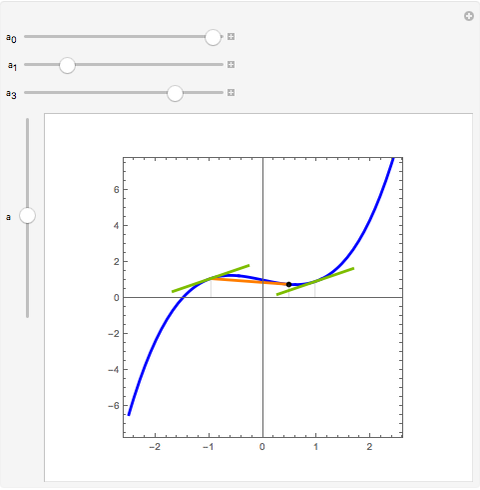
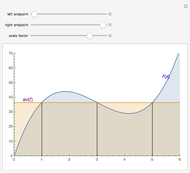
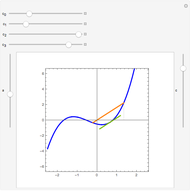
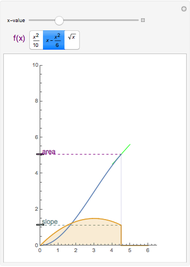
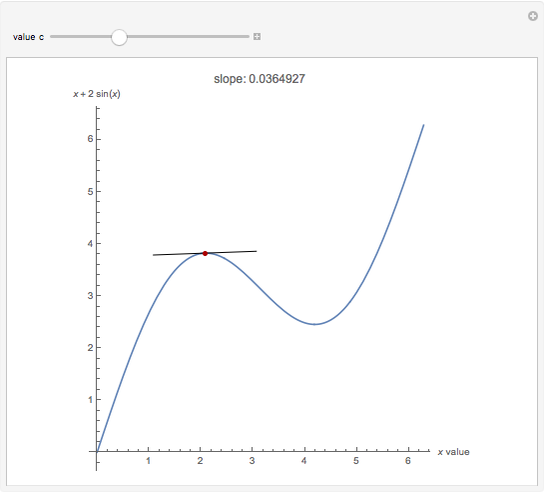
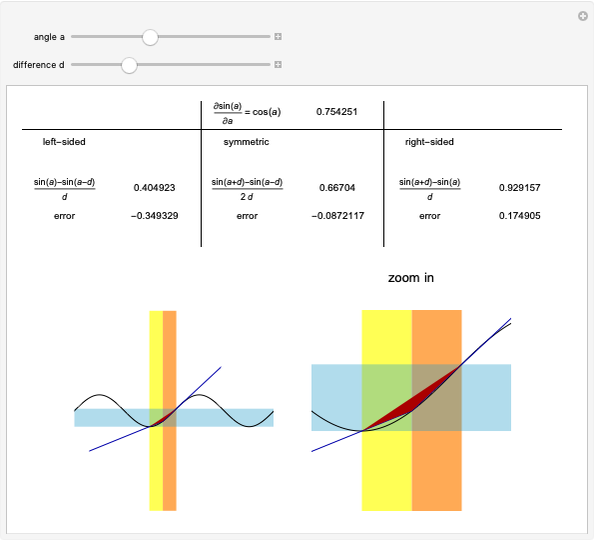
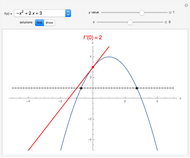
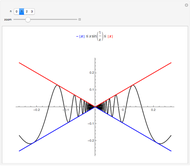
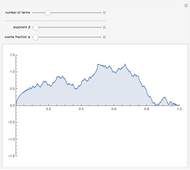
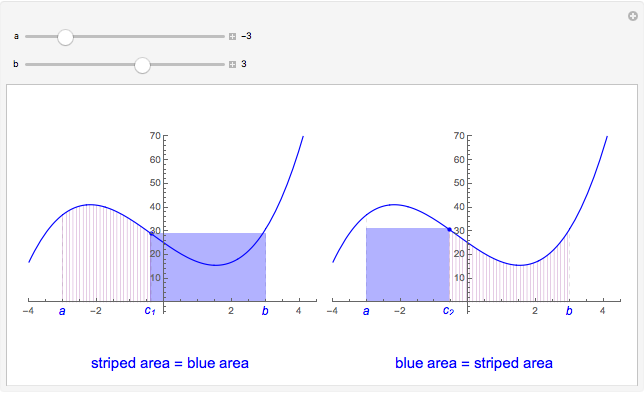
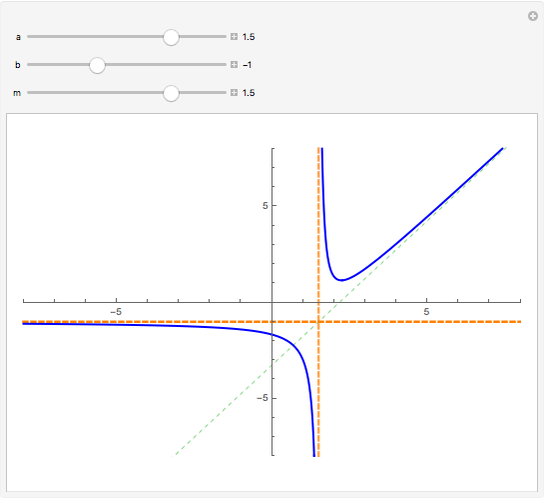
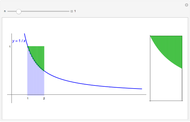
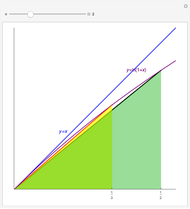
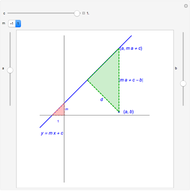
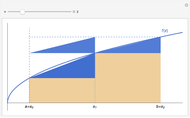
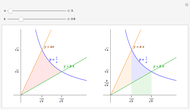
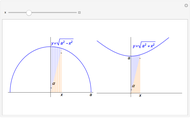
Flett's theorem: Given a function differentiable on with , there is an intermediate point such that

Snapshots

Reference

T. M. Flett, "A Mean Value Theorem," Math. Gazette, 42, 1958 pp. 38–39.


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send