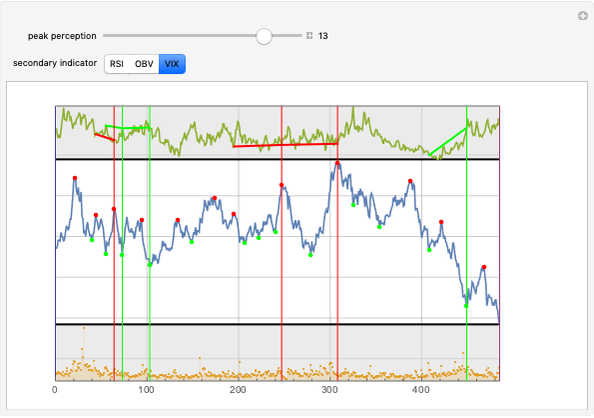
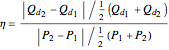The Price Elasticity of Demand

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
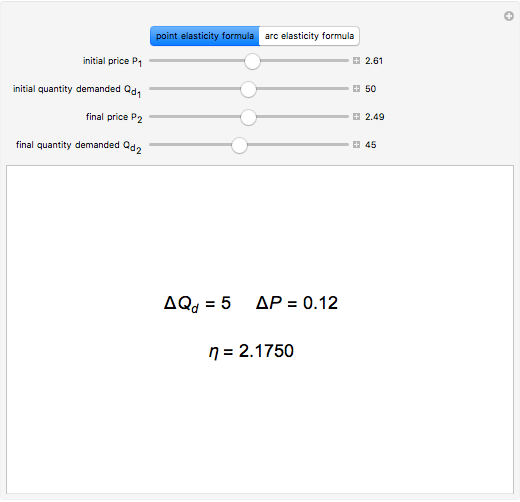
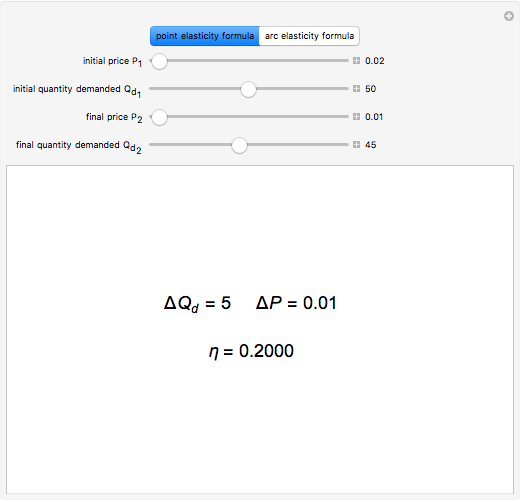
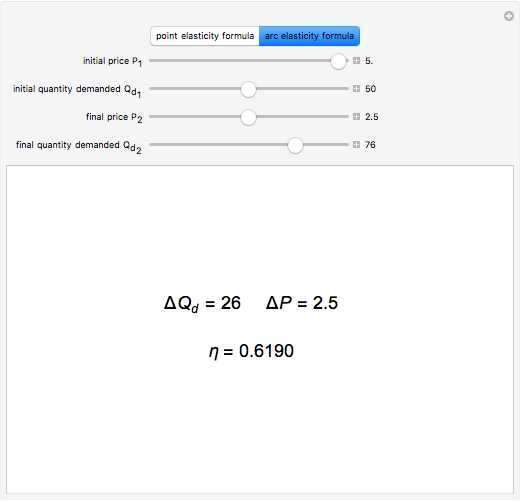
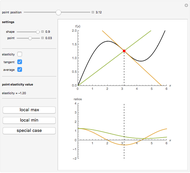
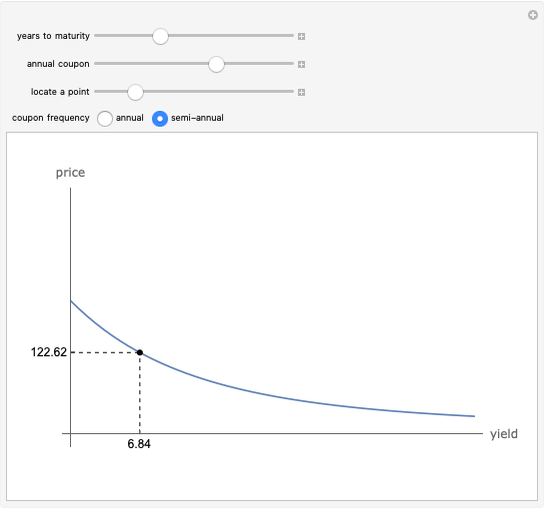
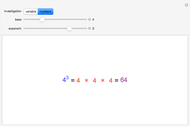
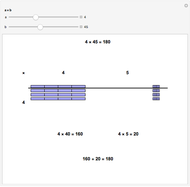
The price elasticity of demand is defined by 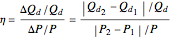 , where
, where 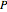 is the price and
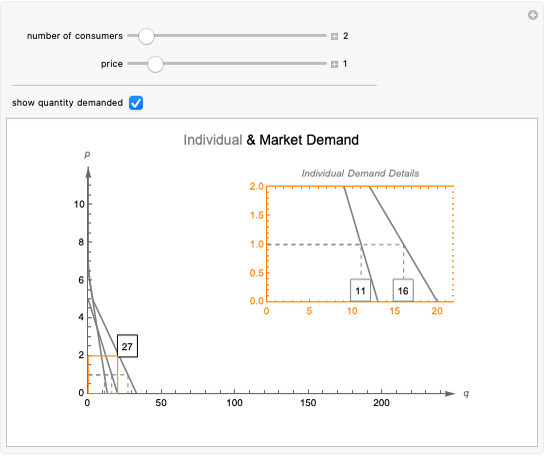
is the price and 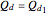 is the quantity demanded. The price elasticity is a measure of how sensitive the quantity demand is to changes in the price.
is the quantity demanded. The price elasticity is a measure of how sensitive the quantity demand is to changes in the price.
Contributed by: Sarah Lichtblau (March 2011)
Open content licensed under CC BY-NC-SA
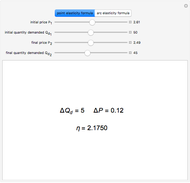
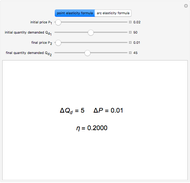
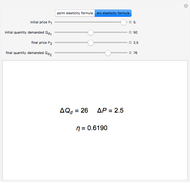
Snapshots
Details
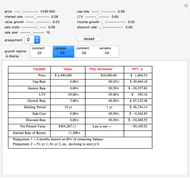
The point elasticity refers to elasticity between two points on the demand curve, not the derivative of the demand curve at a point. The arc elasticity method is also known as the midpoint method.
Note that if 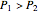 ,
, 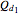 can be greater than
can be greater than 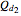 , which is not possible in the real world.
, which is not possible in the real world.
Permanent Citation