The Tangent Line Problem
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
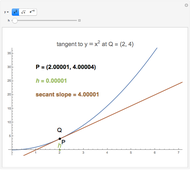
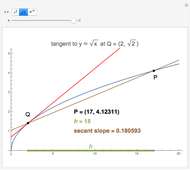
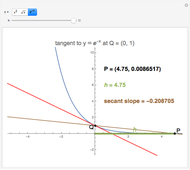
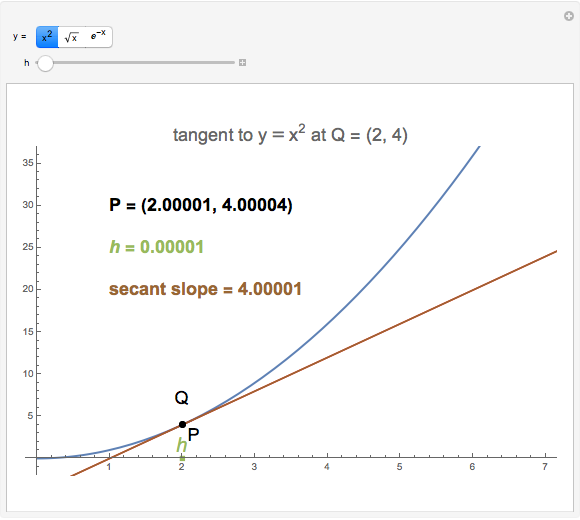
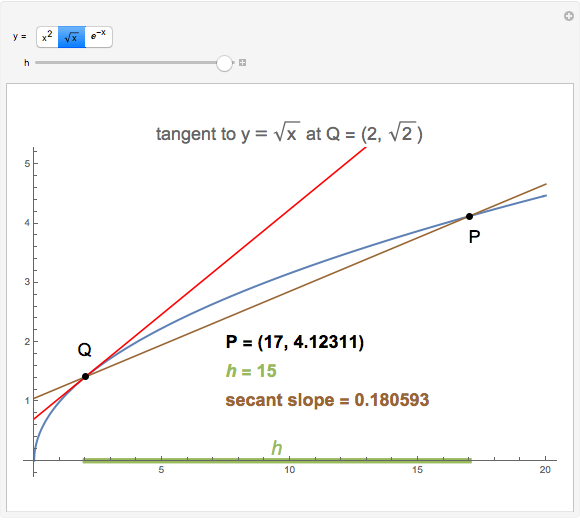
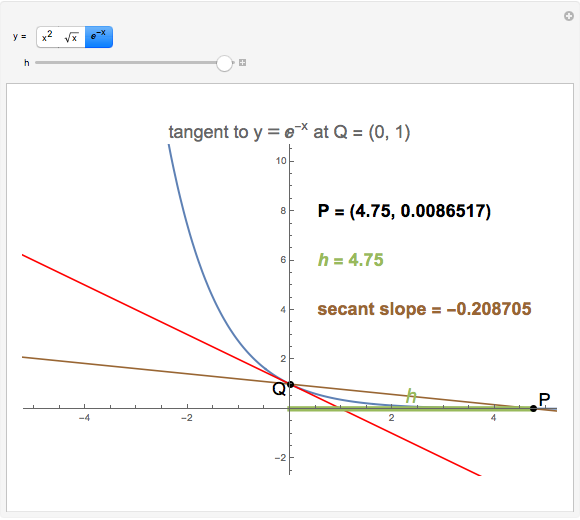
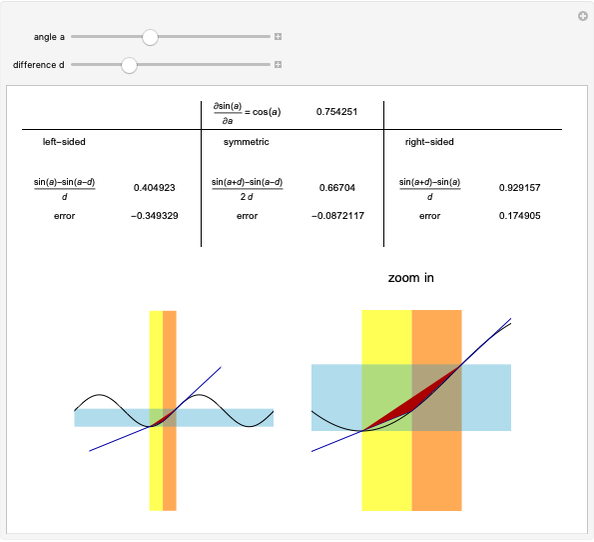
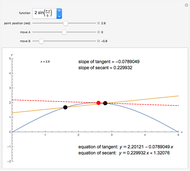
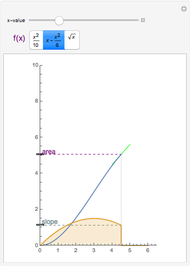
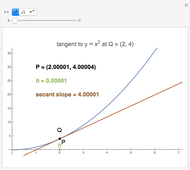
How do you find the slope of the tangent line to a function at a point Q when you only have that one point? This Demonstration shows that a secant line can be used to approximate the tangent line. The secant line PQ connects the point of tangency to another point P on the graph of the function. As the distance 
between the two points decreases, the secant line becomes closer to the tangent line.
Contributed by: Samuel Leung and Michael Largey (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
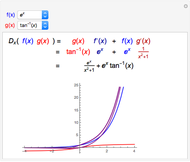
Usually, the slope of a line through two points 
and 
is calculated using the formula 
. This method, however, requires that you know two points; in the tangent line problem, you know only one point. In this case, the slope of the tangent line can be approximated through the use of a limit, 
, where is the horizontal distance between the point of tangency and another point. This Demonstration lets you manipulate the value of and shows how this affects the slope of the secant line.
Permanent Citation
Tangent Planes to Quadratic Surfaces
Gerhard Schwaab and Chantal Lorbeer
Tangent to a Surface
Jeff Bryant and Yu-Sung Chang
Approximating the Derivative by the Symmetric Difference Quotient
Michael Schreiber
Mean Value Theorem
Michael Trott
Approximating the Tangent to a Curve with Secants
Stephen Wilkerson (Towson University)
Directional Derivatives in 3D
Abby Brown
The Quotient Rule
Chris Boucher
The Product Rule
Chris Boucher
The Fundamental Theorem of Calculus
Chris Boucher
Partial Derivatives in 3D
Abby Brown
