The Quotient Rule

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
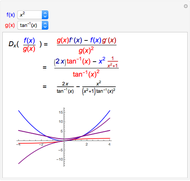
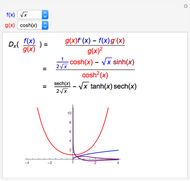
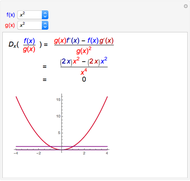
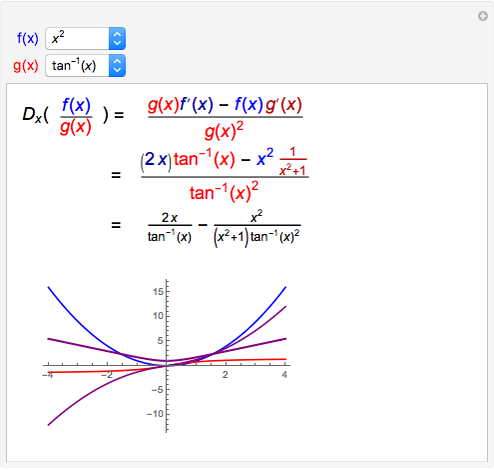
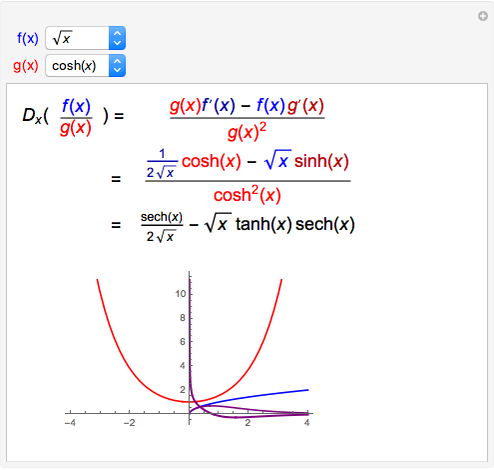
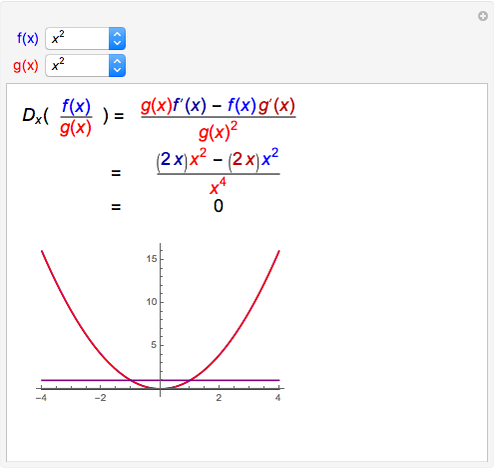
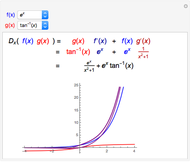
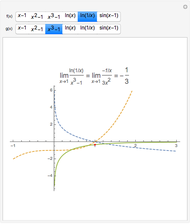
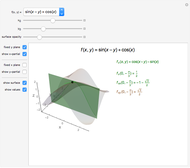
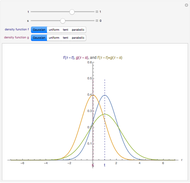
If 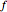 and
and  are both differentiable at
are both differentiable at  and
and 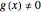 , then the derivative of their quotient at
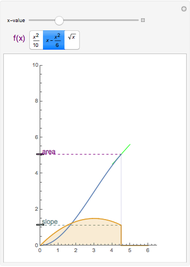
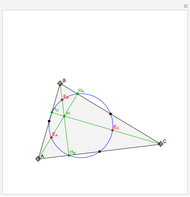
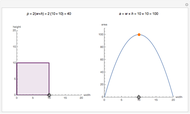
, then the derivative of their quotient at  is given by the quotient rule shown above. On the graph,
is given by the quotient rule shown above. On the graph, 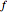 is blue,
is blue,  is red,
is red, 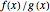 is purple, and the derivative of
is purple, and the derivative of 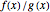 is thick purple.
is thick purple.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"The Quotient Rule"
http://demonstrations.wolfram.com/TheQuotientRule/
Wolfram Demonstrations Project
Published: March 7 2011