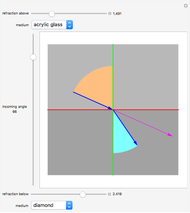
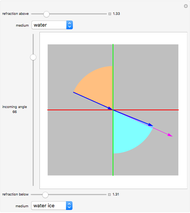
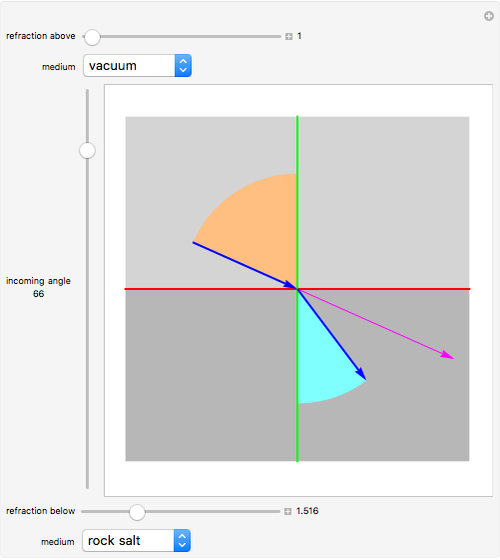
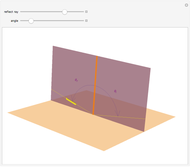
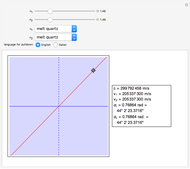
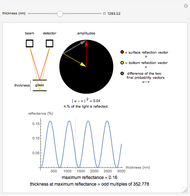
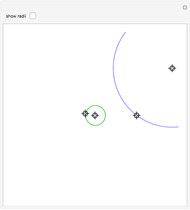
A ray of light is bent on passing from air to a liquid because its wavefront moves more slowly in water than in air. This change in angle is proportional to the propagation velocities, which are often specified by giving the refractive indices of the materials. By definition, a vacuum has a refractive index of 1.
In passing from a slow to a fast medium, total reflection will occur if the angle between the incoming ray and the normal vector of the boundary surface is larger than the critical angle. In that case the incoming angle is equal to the outgoing angle.
The red line indicates the surface boundary which is hit by a ray, and the green line shows its normal vector. The angle between the ray and the surface normal is shown as an orange disk segment. The angle between refracted or reflected rays and the surface normal is shown as a cyan disk segment.
Browse all topics
