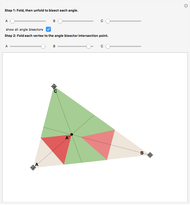
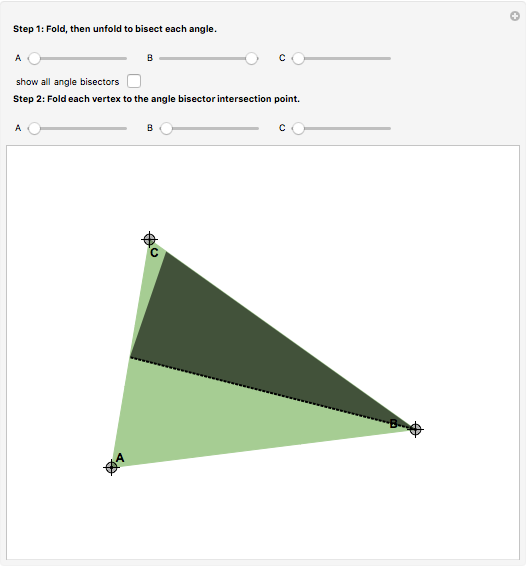
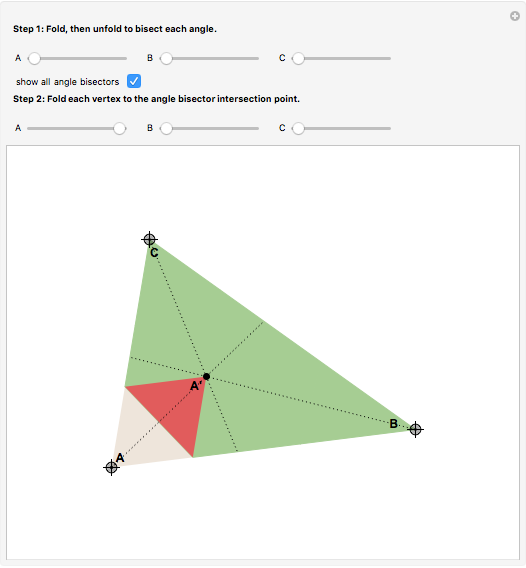
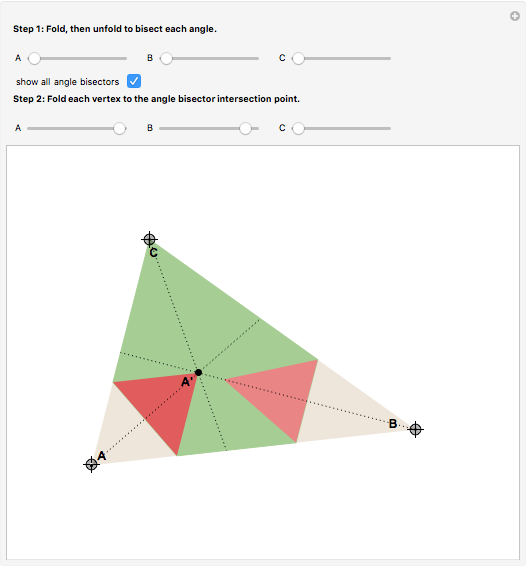
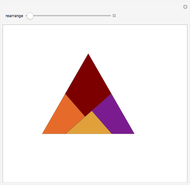
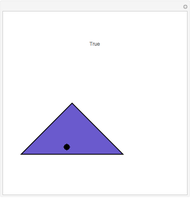
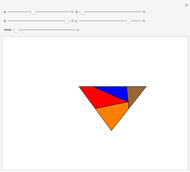
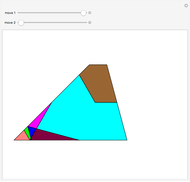
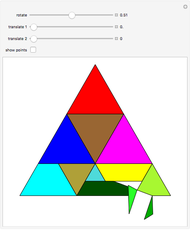
In the Euclidean plane, the measures of the interior angles of any triangle sum to 180 degrees. This can be demonstrated by paper folding. First, bisect each angle to find the intersection point of the three angle bisectors. Second, fold each vertex to this point to see that twice the angle sum is 360 degrees.
The intersection of the three angle bisectors is called the incenter of the triangle. Folding the vertices to the incenter forms three pairs of vertical angles.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
