Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

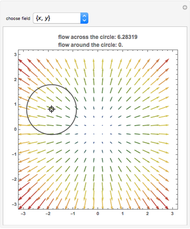
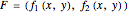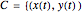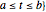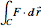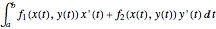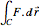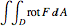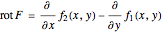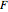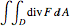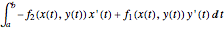Vector Field Flow through and around a Circle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

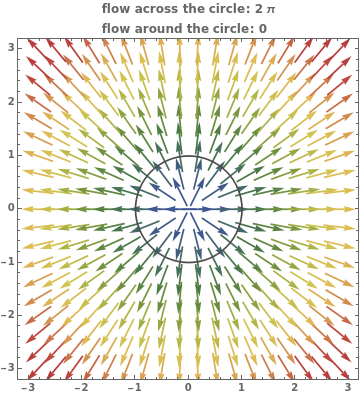
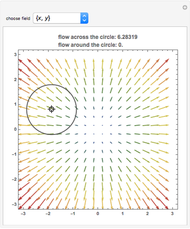
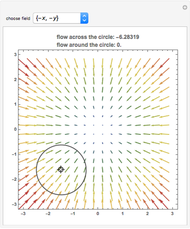
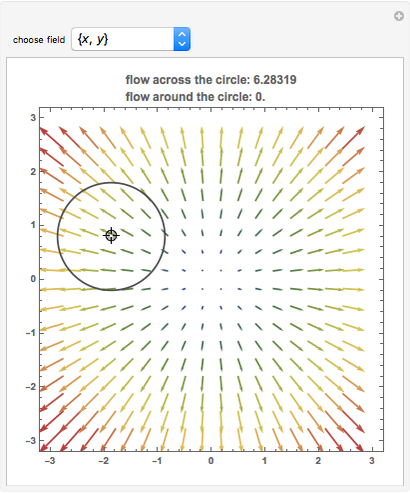
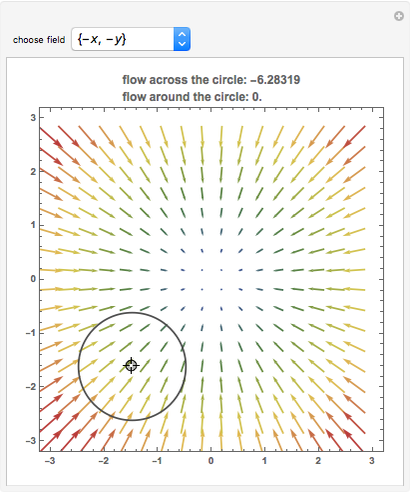
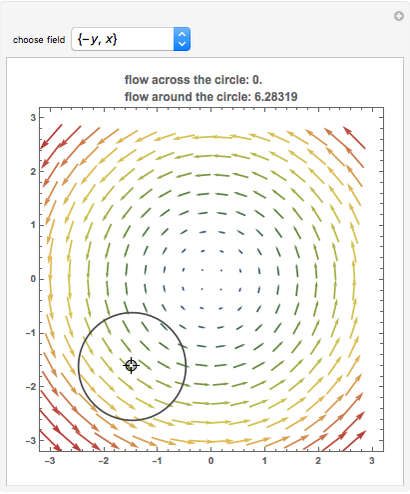
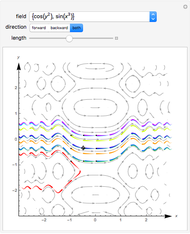
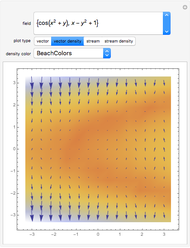
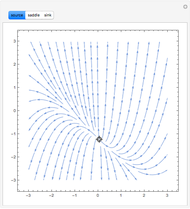
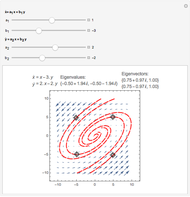
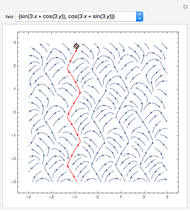
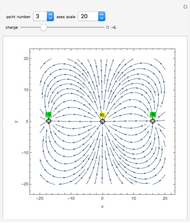
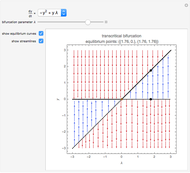
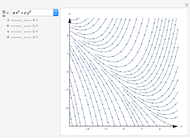
The vector flow across a circle depends on the divergence of the given field: it is always zero when there are no sinks, sources, or singularities. Similarly, the vector flow around the circle depends on rotation (or curl). Here the circle is taken as parametrized in the counterclockwise sense.

[more]

The flow of the vector field along the curve , is given by the line integral , which can also be written as .

Using Green's theorem, the flow along a closed curve is = , where is the region enclosed by the curve and the rotation of the vector field is .

The flow of the vector field across the given closed curve is

= ,

where the divergence of the vector field is .

If the divergence or rotation is constant, the flow across or around any closed curve is constant, too. For example, if the divergence depends only on , like , dragging the circle to the left or right does not change the flow.

[less]

Contributed by: Gosia Konwerska (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send