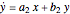Phase Portrait and Field Directions of Two-Dimensional Linear Systems of ODEs
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
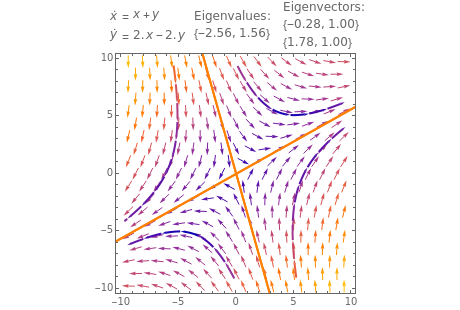
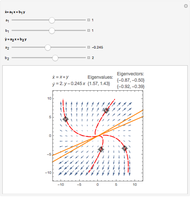
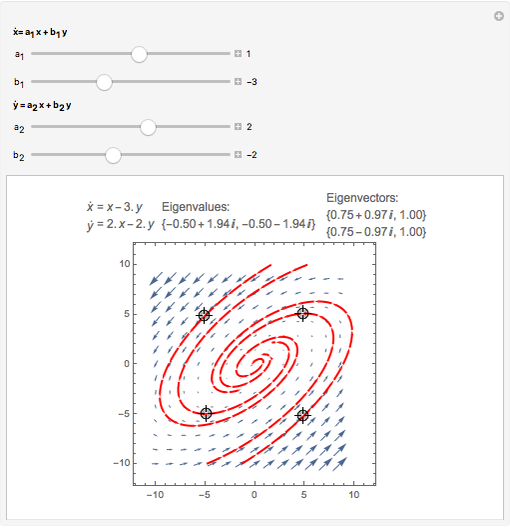
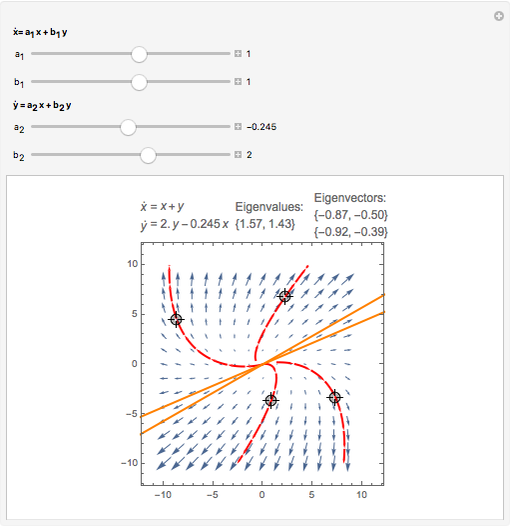
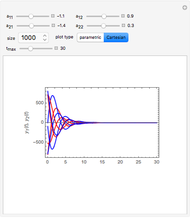
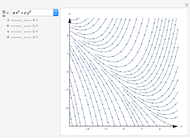
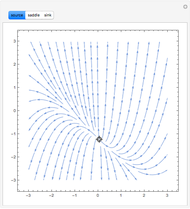
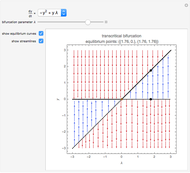
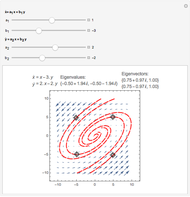
This Demonstration plots the phase portrait (or phase plane) and the vector field of directions around the fixed point 
of the two-dimensional linear system of first-order ordinary differential equations
Contributed by: Santos Bravo Yuste (March 2011)
Open content licensed under CC BY-NC-SA
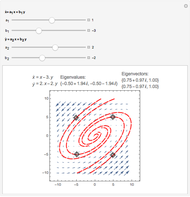
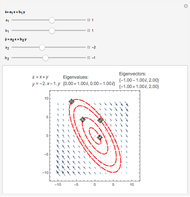
Snapshots
Details
For more information on phase portraits and types of fixed points for linear systems of ODEs, see, for example:
S. H. Strogatz, Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, Cambridge: Westview Press, 2000.
G. F. Simmons, Differential Equations with Applications and Historical Notes, New York: McGraw-Hill, 1991.
Permanent Citation
Visualizing the Solution of Two Linear Differential Equations
Mikhail Dimitrov Mikhailov
Families of Solutions for ODEs
Gosia Konwerska
Flow of a Vector Field in 2D
Gosia Konwerska
Vector Field Flow through and around a Circle
Gosia Konwerska
Sources, Saddle Points, and Sinks in Vector Fields
Gosia Konwerska
Integrating a Vector Field along a Curve
Gosia Konwerska
Bifurcation Diagrams with Flow Fields
Suba Thomas
Slope Fields
Charles E. Oelsner
Vector Fields: Plot Examples
Gosia Konwerska
Vector Fields: Streamline through a Point
Gosia Konwerska
-
Eigenfunctions and Energies for Sloped-Bottom Square-Well Potential
Santos Bravo Yuste -
Sensitivity to Initial Conditions for the Logistic Map
Santos Bravo Yuste -
Numerical Solution of Some Fractional Diffusion Equations
Santos Bravo Yuste -
Phase Portrait and Field Directions of Two-Dimensional Linear Systems of ODEs
Santos Bravo Yuste