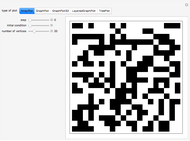
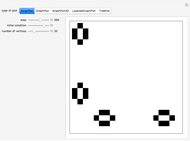
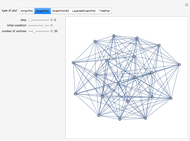
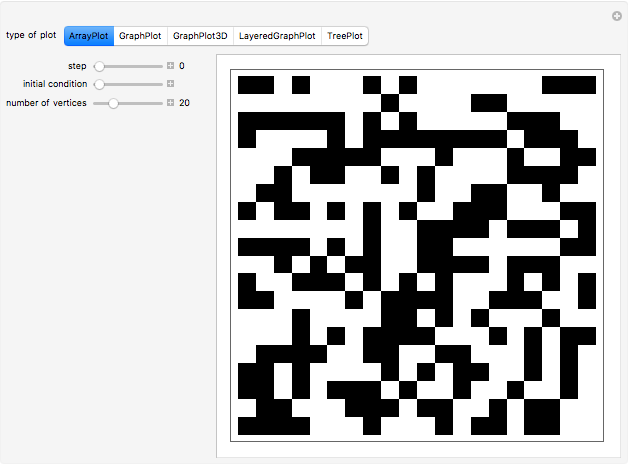
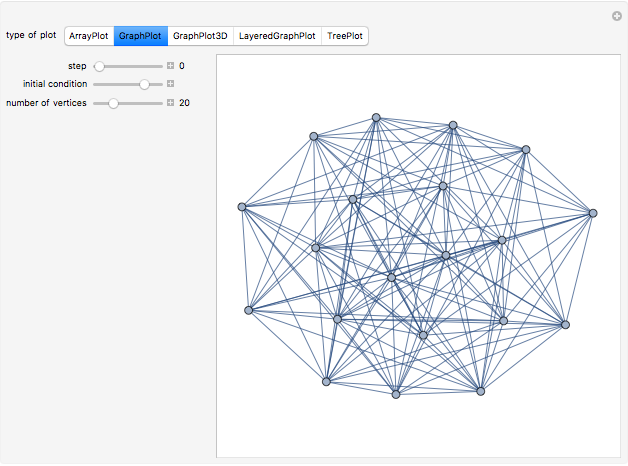
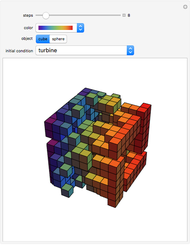
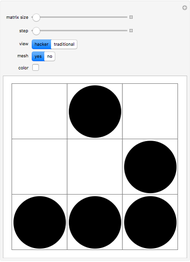
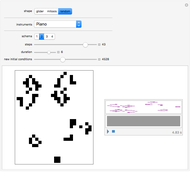
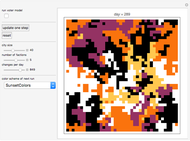
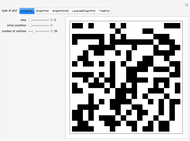
What do Conway's game of life and graph theory have in common? They both can be represented by binary matrices: in Conway's game of life, a 1 represents a live cell (black) and a 0 represents a dead cell (white); likewise, a graph can be represented by its adjacency matrix, where a 0 or 1 represents no link or a link between two nodes, respectively. Applying a nine-cell two-dimensional outer totalistic rule on a random binary square matrix simulates the evolution of the game of life as well as the evolution of a random network. Thus, although the underlying rule is identical in each case, the computation can be represented graphically in many different ways.