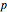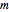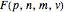Pascal-like Triangles Made from a Game

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
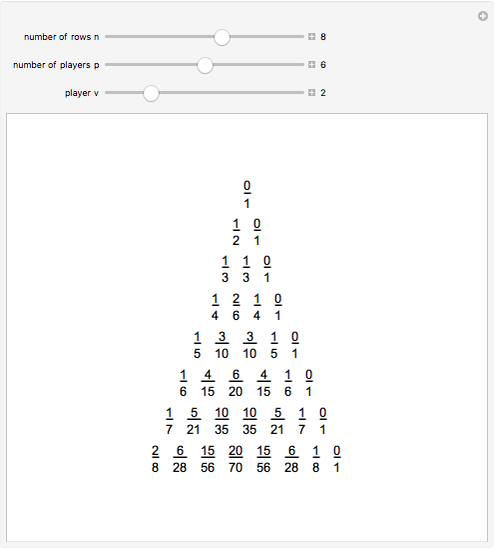
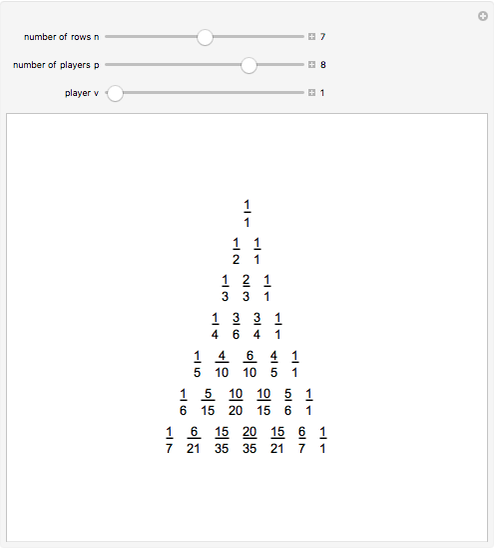
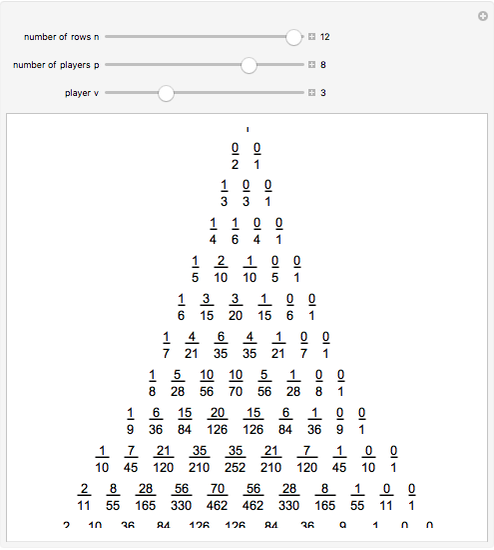
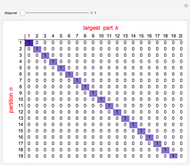
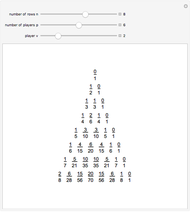
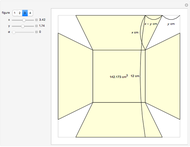
The triangle of fractions has properties that makes it very similar to Pascal's triangle: suppose two adjacent fractions in the same row are  and
and  . Then the fraction below them is
. Then the fraction below them is  , which is how the fractions
, which is how the fractions  and
and  are added in the Farey sequence.
are added in the Farey sequence.
Contributed by: Hiroshi Matsui, Toshiyuki Yamauchi, Daisuke Minematsu, and Ryohei Miyadera (September 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
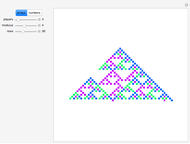
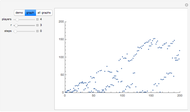
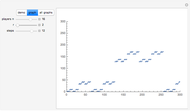
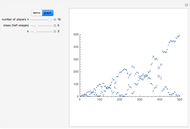
Originally this game was studied as a game of Russian roulette.
For the mathematical background see T. Hashiba, Y. Nakagawa, T. Yamauchi, H. Matsui, S. Hashiba, D. Minematsu, M. Sakaguchi, and R. Miyadera, "Pascal-like Triangles and Sierpinski-like Gaskets," Visual Mathematics: Art and Science Electronic Journal of ISIS-Symmetry [online], 9(1), 2007.
Permanent Citation