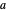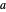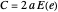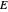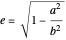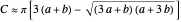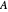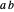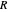Theorems of Pappus on Surfaces of Revolution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
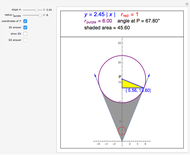
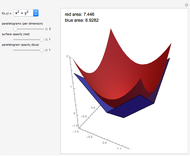
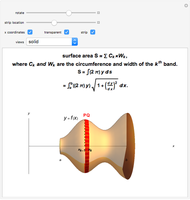
Long before the invention of calculus, Pappus of Alexandria (ca. 290-350 AD) proposed two theorems for determining the area and volume of surfaces of revolution. Pappus's first theorem states that the area of a surface generated by rotating a figure about an external axis a distance  from its centroid equals the product of the arc length
from its centroid equals the product of the arc length  of the generating figure and the distance traversed by the figure's centroid,
of the generating figure and the distance traversed by the figure's centroid, 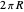 . Thus the area of revolution is given by
. Thus the area of revolution is given by  .
.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
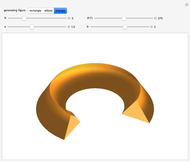
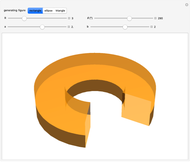
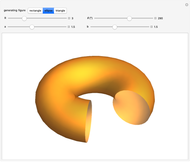
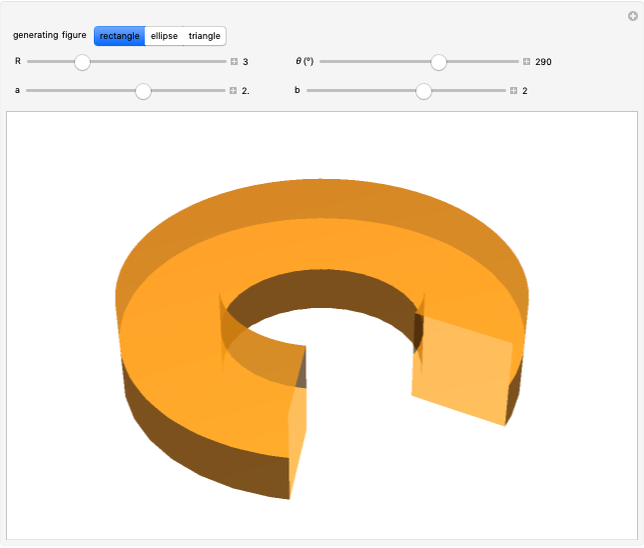
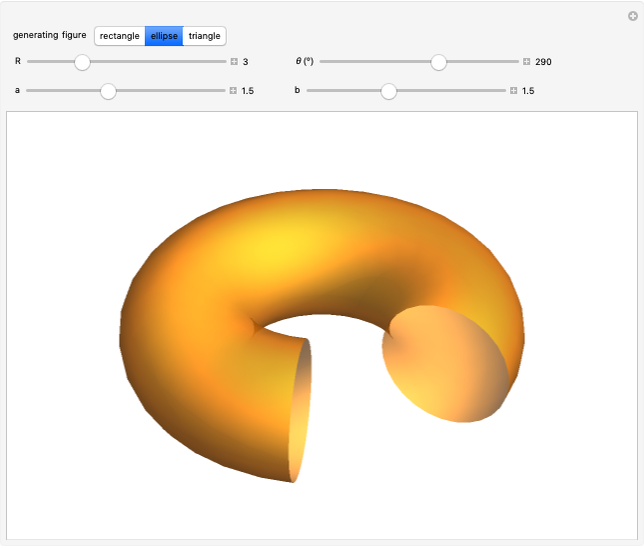
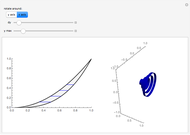
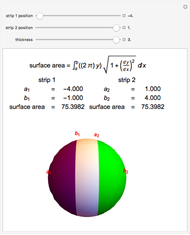
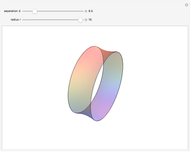
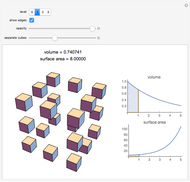
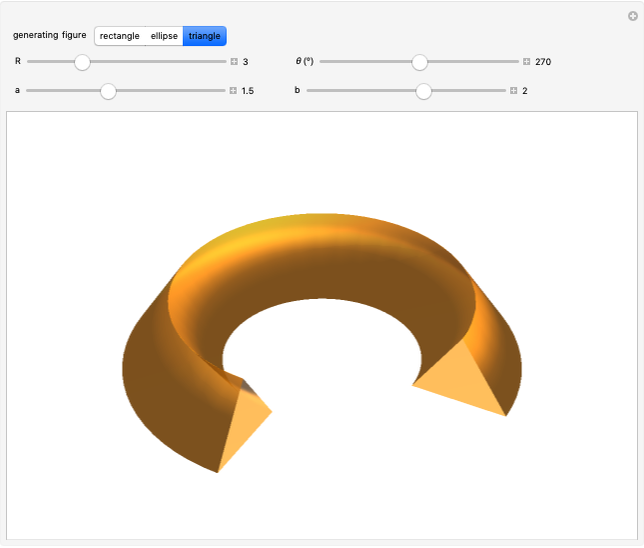
Here are the theorems of Pappus for the most symmetrical cases,  :
:
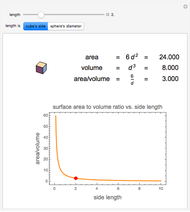
Snapshot 1: a square: volume =  , area =
, area = 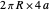
Snapshot 2: a torus: generating figure is a circle of radius  : volume =
: volume =  , area =
, area = 
Snapshot 3: an equilateral triangle: volume =  , area =
, area = 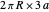
Reference: S. M. Blinder, Guide to Essential Math, Amsterdam: Elsevier, 2008 p. 4.
Permanent Citation