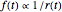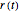Zipf's Law for Natural Languages

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
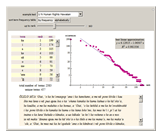
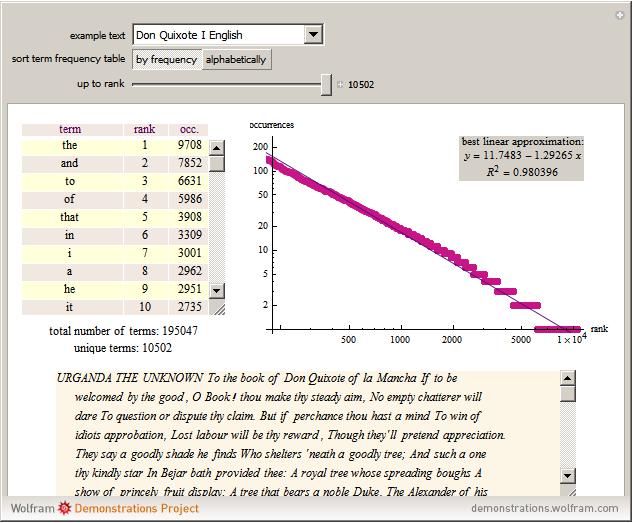
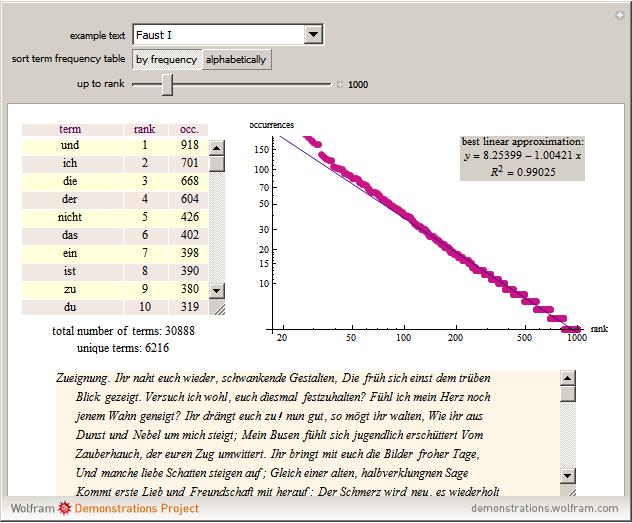
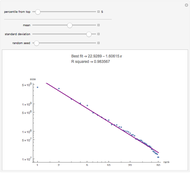
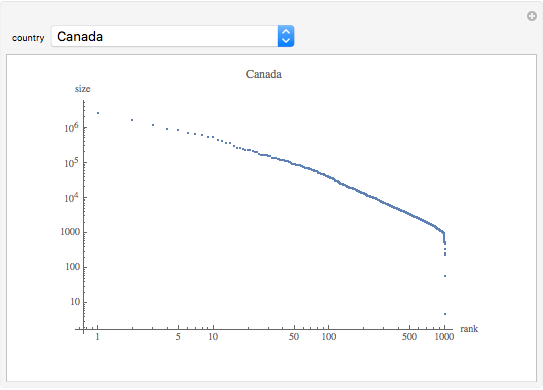
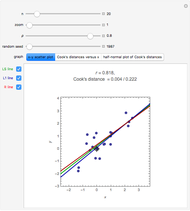
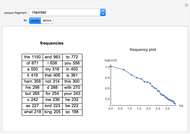
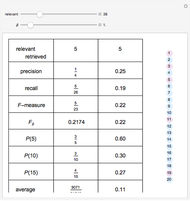
Zipf's law for natural languages states that the frequency of a word is inversely proportional to its rank in the frequency table. The law was originally proposed in the beginning of the twentieth century by George Kingsley Zipf for the English language.
[more]
Contributed by: Giovanna Roda (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: C. D. Manning and H. Schütze, Foundations of Statistical Natural Language Processing, Cambridge, MA: MIT Press, 1999.
Permanent Citation
"Zipf's Law for Natural Languages"
http://demonstrations.wolfram.com/ZipfsLawForNaturalLanguages/
Wolfram Demonstrations Project
Published: March 7 2011