Exploring Measures of Association

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
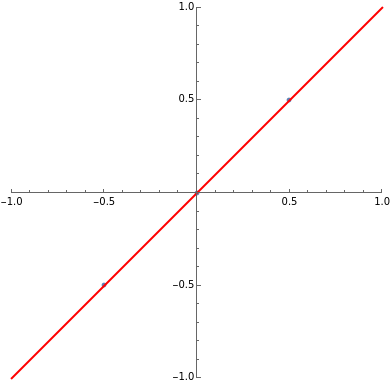
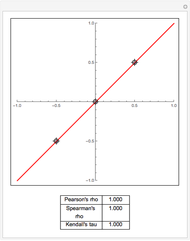
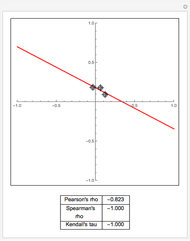
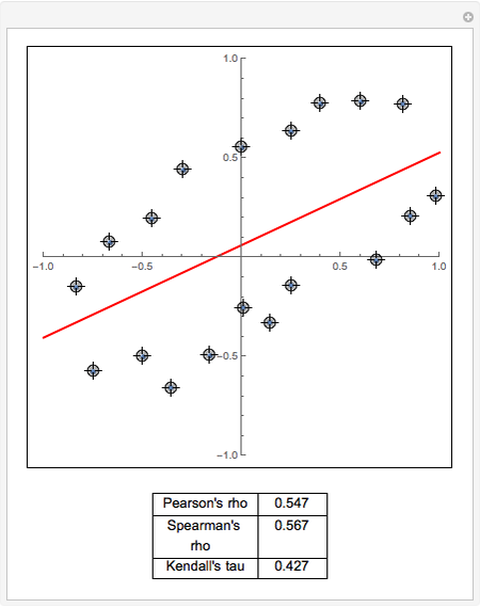
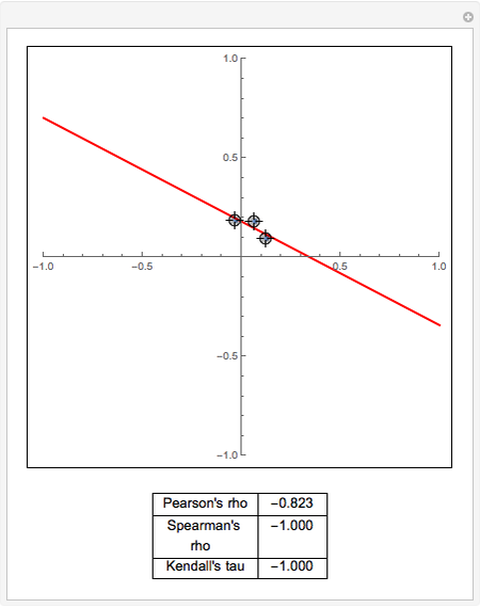
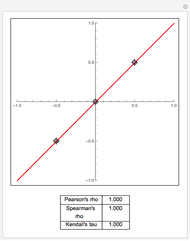
Using Alt-Click, add additional data points to the scatter plot above or drag the existing data points. The least-squares linear fit to the data changes as you add additional data points or drag them. Additionally, three sample measures of dependence between the 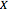 and
and  coordinates of the data are summarized (viewing the coordinate projections as realizations from a pair of random variables).
coordinates of the data are summarized (viewing the coordinate projections as realizations from a pair of random variables).
Contributed by: Jeff Hamrick (August 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Pearson's correlation coefficient is a popular measurement of association between two random variables. It characterizes the extent to which a pair of random variables  can be written as
can be written as  , where
, where 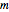 and
and  are real-valued constants. Unfortunately, the Pearson correlation coefficient completely characterizes the dependence structure between two random variables only when the joint distribution of those random variables is elliptical. In general, elliptical distributions are those distributions with constant curves in
are real-valued constants. Unfortunately, the Pearson correlation coefficient completely characterizes the dependence structure between two random variables only when the joint distribution of those random variables is elliptical. In general, elliptical distributions are those distributions with constant curves in 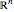 that are ellipsoids. Additionally, the Pearson correlation coefficient only captures the first-order, or linear, association between two random variables.
that are ellipsoids. Additionally, the Pearson correlation coefficient only captures the first-order, or linear, association between two random variables.
There are numerous additional nonlinear measures of association. Some are finite dimensional and others are infinite dimensional. Two additional finite-dimensional measures of association are Spearman's rho and Kendall's tau.
Spearman's rho is similar to Pearson's rho, but is computed on the ranks of the original data. Kendall's tau is equal to 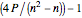 , where
, where  is the number of concordant pairs. If
is the number of concordant pairs. If  and
and 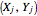 are a pair of bivariate observations of a random vector
are a pair of bivariate observations of a random vector  , then this pair is concordant if
, then this pair is concordant if 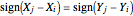 . So if we have
. So if we have  observations of the random vector
observations of the random vector  , we must determine if up to
, we must determine if up to 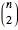 pairs are concordant.
pairs are concordant.
Infinite-dimensional measures of dependence include copulas and the local correlation function developed by Bjerve and Doksum (1993).
For more information on Spearman's rho and Kendall's tau, see the Wikipedia entries.
Permanent Citation