15-Point Projective Space

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
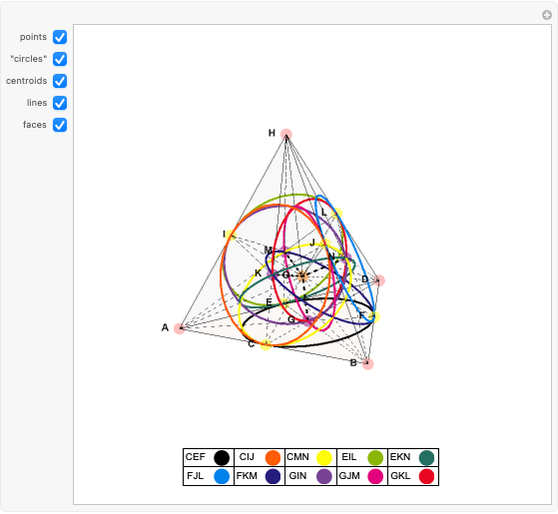
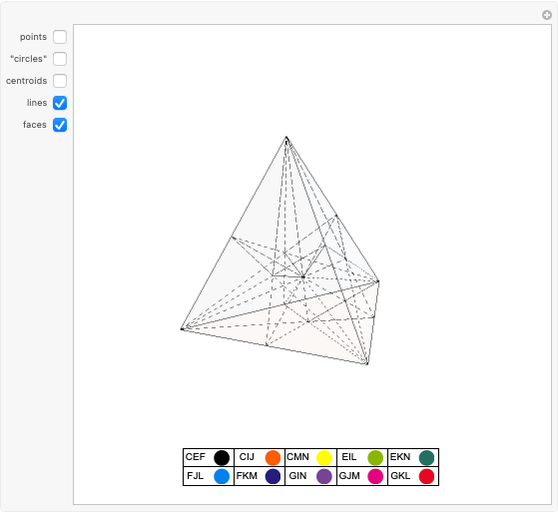
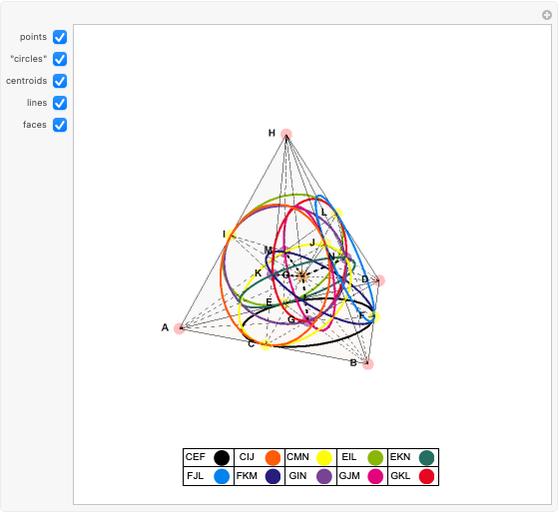
This Demonstration shows a representation of the smallest projective 3-space, that is, the smallest geometry that satisfies the postulates of incidence and existence of synthetic projective geometry and that can be coordinatized by four homogeneous coordinates. It contains 15 points, 15 planes, and 35 lines. Each line is incident with exactly three points. Each plane is a Fano plane. No particular analytic geometric meaning should be attached to the diagram, although it is useful for visualizing symmetries. This space is known as  , the 3D projective space over the field of integers mod 2,
, the 3D projective space over the field of integers mod 2,  .
.
Contributed by: John Hurley (March 2011)
Open content licensed under CC BY-NC-SA
Details
Synthetic projective geometry is a system based on a set of postulates, where points and lines are undefined elements. Postulates of incidence define how points and lines are related, and postulates of existence eliminate trivial cases. It can be shown that the smallest 3-space that satisfies the set of postulates contains 15 points. The smallest projective plane (i.e. 2-space) contains seven points and seven lines and is known as the Fano plane.
Some of the lines are shown as "circles"; one such as CIJ merely means that it is the unique line incident with points C, I, and J.
References
[1] B. Meserve, Fundamental Concepts of Geometry, New York: Dover, 1983.
[2] A. Beutelspacher and U. Rosenbaum, Projective Geometry: From Foundations to Applications, Cambridge: Cambridge University Press, 1998.
[3] B. Polster, A Geometrical Picture Book, New York: Springer, 1998.
[4] "Barycentric Coordinates from Cross- and Dot-Products" in "Circumscribed Circle." (Feb 9, 2011) http://en.wikipedia.org/wiki/Circumcenter.
[5] "Parametric Equation" in "Circumscribed Circle." Wikia. (Aug 14, 2009) http://math.wikia.com/wiki/Circumscribed_circle.
Snapshots
Permanent Citation