Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Inverse Stereographic Projection of Simple Geometric Shapes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

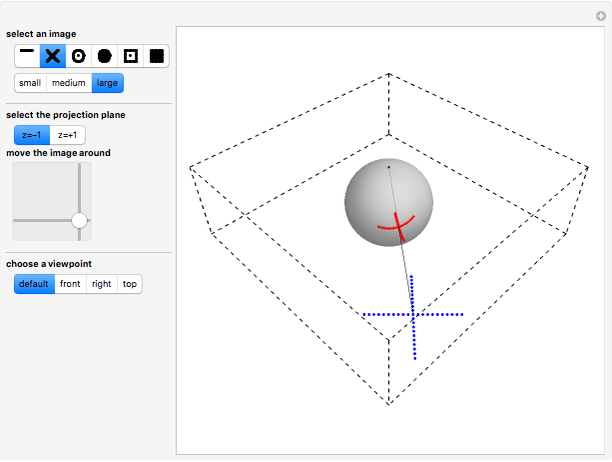
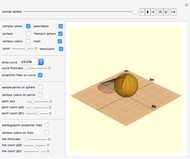
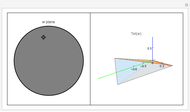
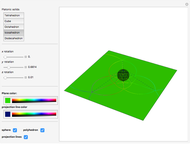
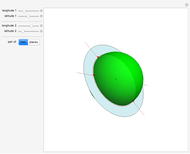
This Demonstration highlights the properties of stereographic projection. This is achieved by mapping simple geometric shapes from the or 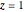plane onto the unit sphere using inverse stereographic projection. The inverse stereographic projection of the point 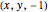to the unit-sphere is the point .

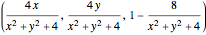Contributed by: Erik Mahieu (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

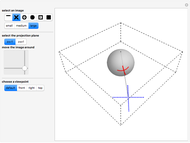
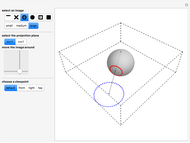
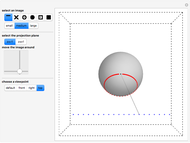
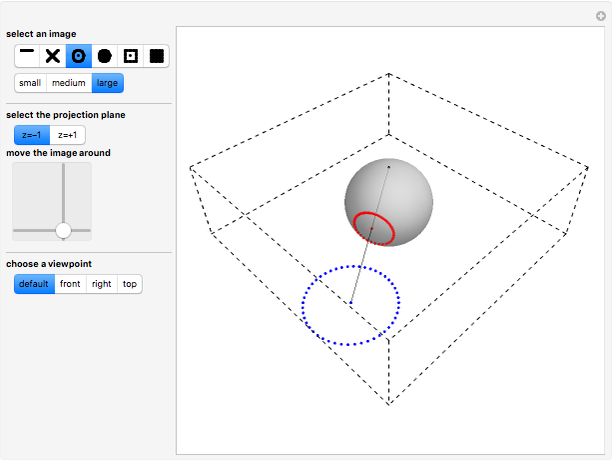
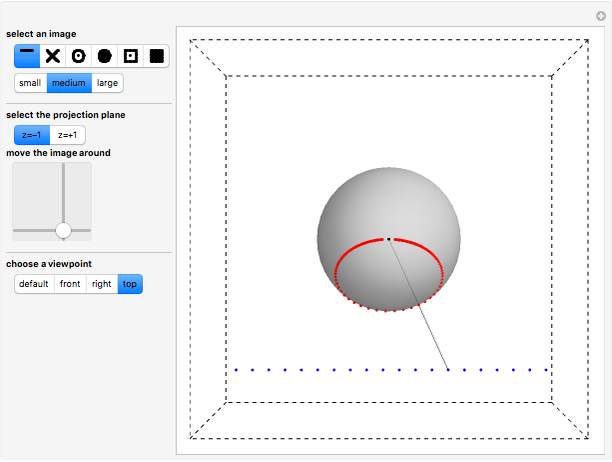
These snapshots illustrate some properties of stereographic projection:

Snapshot 1: preservation of angles (conformality)

Snapshot 2: circles in the plane are mapped to circles on the sphere

Snapshot 3: lines in the plane are mapped to great circles on the sphere

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send