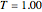2D Heat Diffusion Using a Search-Update-Feedback Cellular Automaton (SCA) Approach

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
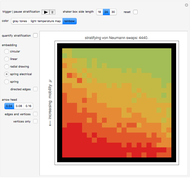
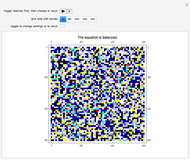
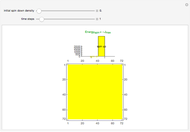
This Demonstration shows heat diffusing in the plane starting from an initially heated cell cluster centered in an otherwise cool 2D slice of material. The code restarts using the same initial conditions when the diffusion of heat is such that the temperature across the plane is largely uniform (the initially cool cells rise on average to some value 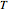 and the initially heated cells fall on average to the same value
and the initially heated cells fall on average to the same value 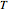 ).
).
Contributed by: Michael Dewus (October 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
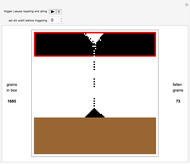
The control "trigger | pause" triggers the SCA; toggle the "reset" control to restart with a new heat source, or check this control to change the diffusion grid size; uncheck "reset" to restart the diffusion.
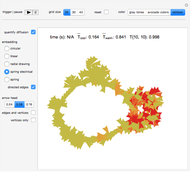
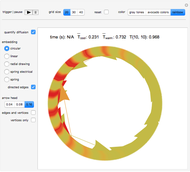
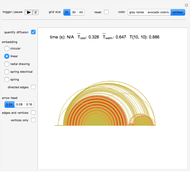
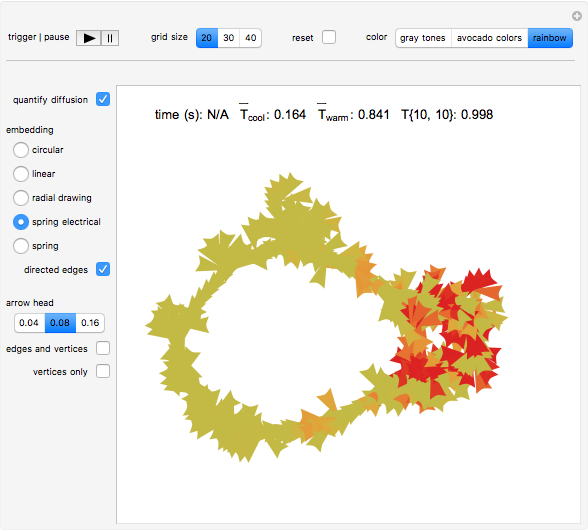
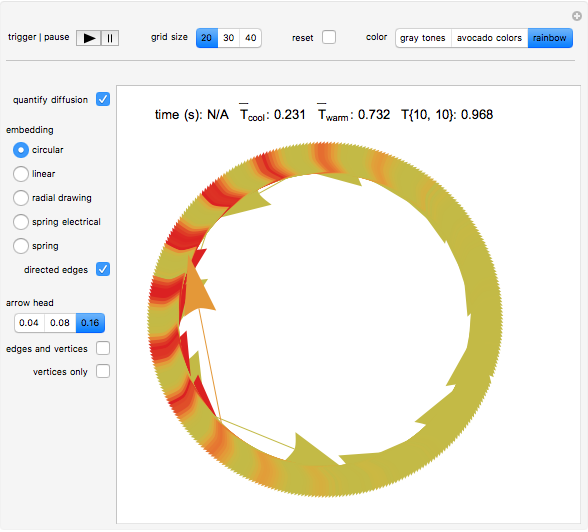
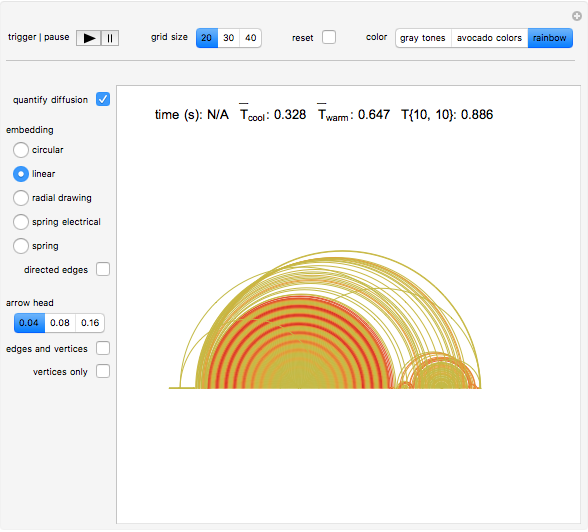
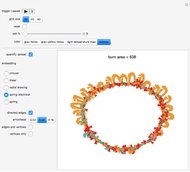
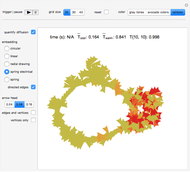
Check the "quantify diffusion" control at any time to switch between the matrix plot simulation of the diffusion and a network quantification of this simulation; the quantification is exhaustive on a per cell basis. Color information is synchronized between these two views; change the color setting at any time.
With "quantify diffusion" checked, check the "directed edges" control to follow the information flow throughout the diffusion grid as the heat dissipates (use the "directed edges" control with any of the network embedding methods; linear embedding is informative with both settings of this control). Edge colors are determined by the datum of the vertex a given arrow points to; vertex formats are shown below.
Use the control "edges and vertices" or "vertices only" to get vertex information (please note that "vertices only" has precedence)—pause and mouseover a vertex of interest to locate it in the diffusion grid. Vertices have this format: {{cell row, cell column}, cell temperature}, where temperature is the vehicle that carries along dissipative heat information.
You can find in section 3 of the code more details concerning the controls.
References
[1] G. Strang, Computational Science and Engineering, Wellesley, MA: Wellesley-Cambridge Press, 2007.
[2] Wikipedia. "Heat Equation." (Sep 4, 2013) en.wikipedia.org/wiki/Heat_equation.
[3] Wikipedia. "Negative Feedback." (Mar 8, 2013)en.wikipedia.org/wiki/Negative_feedback.
[4] Wikipedia. "Positive Feedback." (Mar 8, 2013) en.wikipedia.org/wiki/Positive_feedback.
Permanent Citation