Granular Toppling and Piling

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
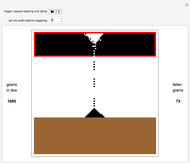
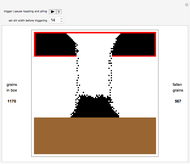
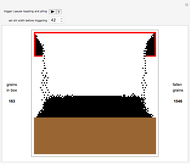
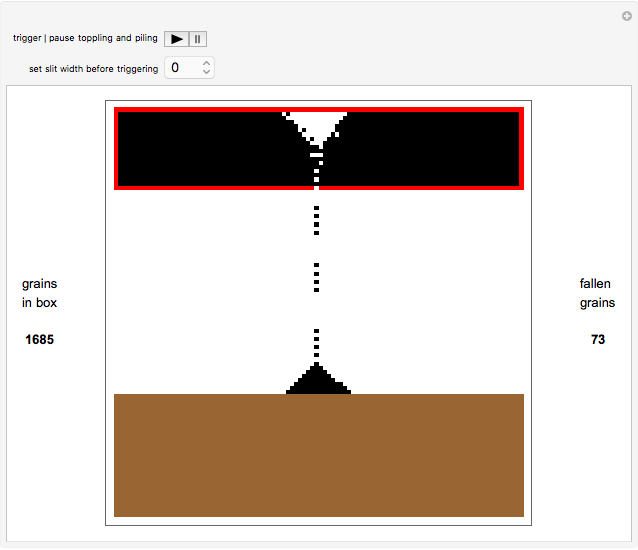
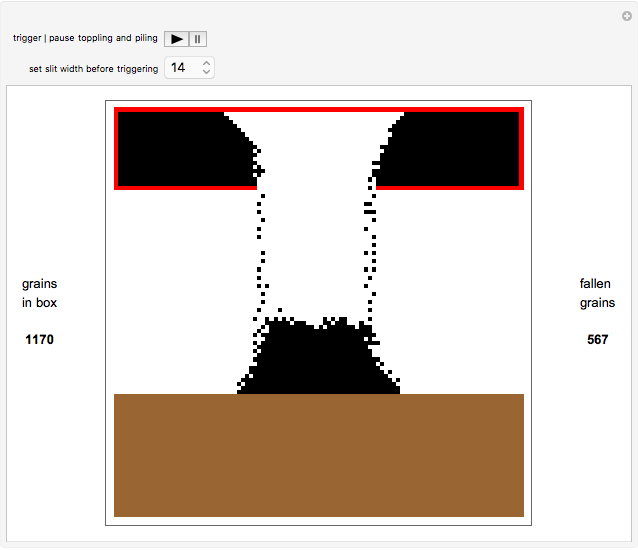
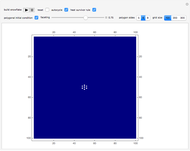
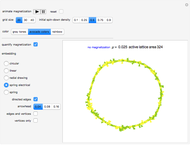
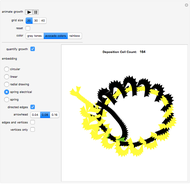
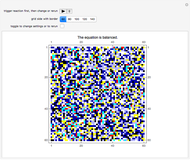
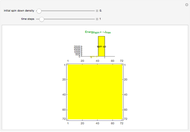
This Demonstration shows the toppling and piling tendencies of ideal grains of uniform geometry under ideal conditions. Toppling is observed both in the red grain box and after the grains hit the ground. At the confluence of grains above the grain box slit friction effects can give rise to arching, forcing the grains to fall through the slit at a nonuniform rate.
Contributed by: Michael Dewus (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This program uses a 2x2 block cellular automaton (BCA) with feedback to achieve its effect. The refresh rules include two major constraints: (1) Granular stability requires that an occupied upper cell remains occupied only if both lower cells of the given block are occupied. (2) A random choice determines how two simultaneously occupied upper cells topple when one of the lower cells of the given block is unoccupied. The BCA outworking of (1) forces a stable angle of repose to manifest at 45° relative to the top of the grain box, while the BCA outworking of (2) provides insight into granular arching tendencies that arise due to inter-grain friction phenomena as grains flow. The counter to the left of the plot counts the number of grains in the grain box, while the counter to the right of the plot counts the number of fallen grains. The "slitwidth" control may be used to vary the slit width—actual slit width is measured in grains, and is 2 times the slitwidth plus 1.
Information Feedback Background
Information feedback is a mechanism, as opposed to information updates, which are events (both in artificial and real systems). Updates, of necessity, may be quite random in time and in space; in fact, nature utilizes this updating randomness very well to its advantage. But feedback proper, as a mechanism, cannot be understood to be random somehow—it is more properly a fundamental and universal algorithm of nature. Accordingly, and importantly, the so-called evolution of most systems in nature appears to be driven by the feedback of refreshed updating events, which comprise refreshed updating information (it is understood that the information is rule sensitive and not driven or forced). Where t is time,
(1) defines feedback of refreshed updating information; by default it is also a succinct computational definition of time: given an arbitrary refresh in the nesting chain besides the first one on the right, the future "refresh-nests" to the left, the past has "refresh-nested" from the extreme right leftward up to and including one refresh to the right of the given arbitrary refresh, and the future and the past intersect in the present, which is the given arbitrary refresh.
Another example (besides the Demonstration) of (1): Given an ice cube melting in one's hand (an irreversible process), the "refresh" dynamic in (1) would be tantamount to "thermodynamics." Notice that feedback is not an overtly discernible mechanism in the Demonstration nor in this example, yet in a highly abstract manner it dominates both of the systems' mechanics, for if the refreshed information were not continuously fed back to the refresh dynamic, the given system could not evolve, it would halt. Such halting happens naturally in systems at some pertinent equilibrium, but not because feedback is no longer operative, but rather because the associated refresh dynamic can no longer transform information. Apparently information feedback in nature is always "on," never "off."
Feedback of rule-based update information is damped (through specific rule constraint), thus it might properly be considered to be negative feedback. More specifically, the four fundamental forces of nature F, individually or as necessary in combination, appropriately birth for a given system the refresh rules R, a function of F, or, R(F), that constrain it ultimately to lower its potential energy V (R(F)= -∇V shows the specific constraint; the more familiar form is F=-∇V—the equations qualify the same principle, one with rule symbolism, the other without it). As such, a hypothesis is set forth: negative system information feedback to R(F) (this mechanism, as in (1) above), not the rule progenitor F, nor even F's end R(F), is the basis of the great conservation principles observed in nature. The hypothesis assumes rule-constrained negative information feedback that is always "on," as said above. This Demonstration is based on rule-constraining negative information feedback in a classical setting (F here is largely gravitational, and R(F) proceeds from that); please see "Magnetization With An Ising Model Based on a Search-Update-Feedback Cellular Automata (SCA) Approach" for an example of information feedback in a nonclassical setting (here F is fundamentally electromagnetic; R(F) is based on the quantum mechanical explanation of F's behavior, and incorporates discretization and energy conservation). It is noteworthy that the implementation of (rule-constrained, negative) feedback is different in these two Demonstrations, yet the effect of the feedback is consistent and as expected.
Reference
[1] B. Chopard and M. Droz, Cellular Automata Modeling of Physical Systems, Cambridge: Cambridge University Press, 2005.
Permanent Citation
"Granular Toppling and Piling"
http://demonstrations.wolfram.com/GranularTopplingAndPiling/
Wolfram Demonstrations Project
Published: February 25 2012