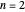A Converging Geometric Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
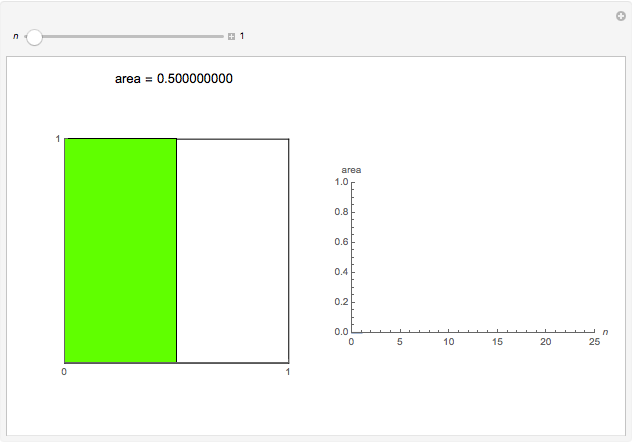
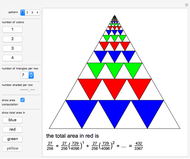
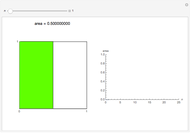
This Demonstration shows that  .
.
Contributed by: Akane Hattori and Natsuki Okuda (June 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
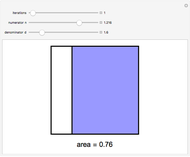
Snapshot 1: when  , the area is filled is
, the area is filled is 
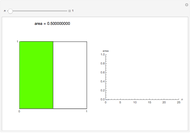
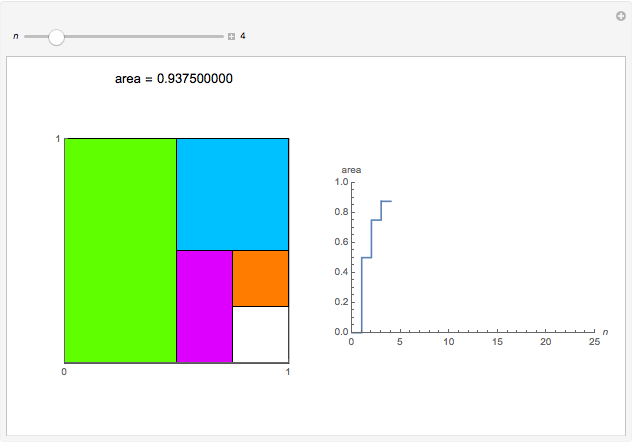
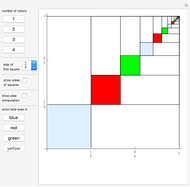
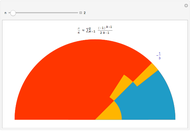
Snapshot 2: when 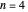 , a square with area
, a square with area 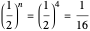 is added
is added
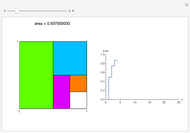
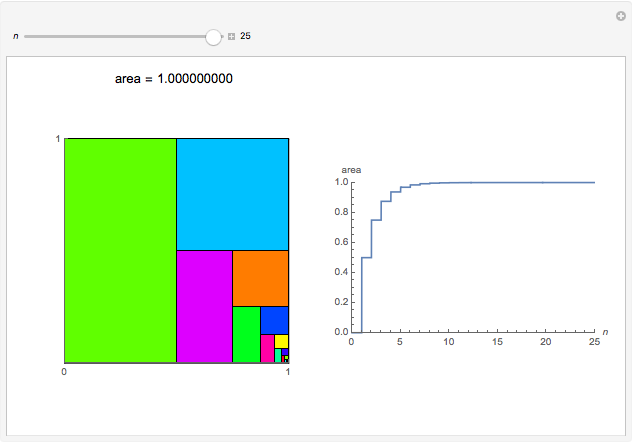
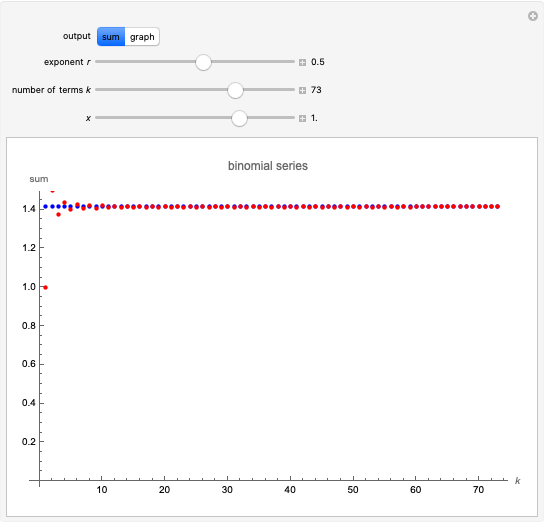
Snapshot 3: where 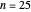 and the area filled is very close to 1
and the area filled is very close to 1
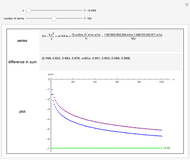
The geometric series  converges if and only if
converges if and only if  , and then the sum of the series is
, and then the sum of the series is  . Convergence of
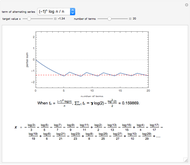
. Convergence of 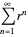 can be proven by the integral test, which states that if
can be proven by the integral test, which states that if 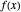 is continuous, decreasing, and positive, then
is continuous, decreasing, and positive, then  converges if
converges if 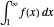 converges. In this case,
converges. In this case,  , so the integral converges and therefore the geometric series also converges.
, so the integral converges and therefore the geometric series also converges.
Special thanks to the University of Illinois NetMath Program and the mathematics department at William Fremd High School.
References
[1] R. Bayer. "Proof By Picture." (Aug. 13, 2009) www.scribd.com/doc/254948592/Proof-by-Picture.
[2] M. Moody. "Convergence Tests for Infinite Series." (Jun 18, 2013) www.math.hmc.edu/calculus/tutorials/convergence.
Permanent Citation