Adding Points on an Elliptic Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
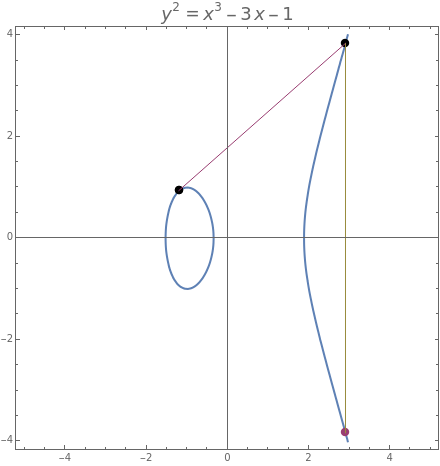
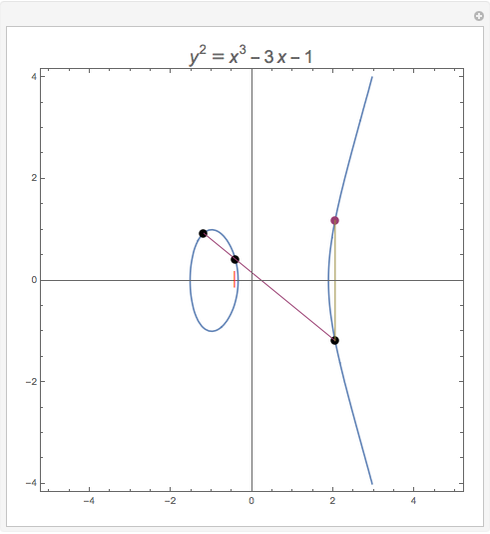
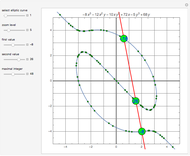
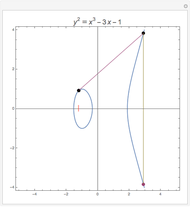
Elliptic curves are the solutions sets of nonsingular cubic polynomials of degree three. It is possible to define an addition law for these points so that they form an abelian algebraic group. In order to add distinct points, construct the line between them and determine the third point of intersection with the curve. The sum of the two points is then the reflection of the third point about the axis of symmetry, which is the  axis for the case illustrated here. In order to add a point to itself, use the tangent line to the curve at that point.
axis for the case illustrated here. In order to add a point to itself, use the tangent line to the curve at that point.
Contributed by: John McGee (March 2011)
Open content licensed under CC BY-NC-SA
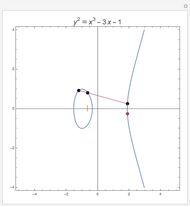
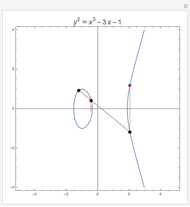
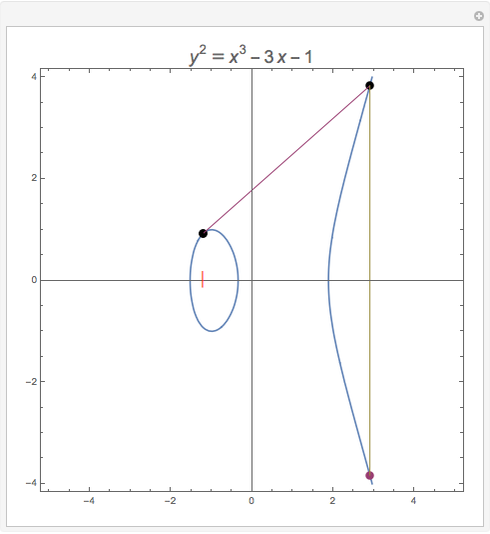
Snapshots
Details
For an introduction to the mathematics and applications of elliptic curves, see L. C. Washington, Elliptic Curves: Number Theory and Cryptography (Discrete Mathematics and Its Applications) [online], Boca Raton, FL: Chapman & Hall/CRC, 2003. http://www.math.umd.edu/~lcw/ec.html.
Permanent Citation
"Adding Points on an Elliptic Curve"
http://demonstrations.wolfram.com/AddingPointsOnAnEllipticCurve/
Wolfram Demonstrations Project
Published: March 7 2011