Anomalies for Planetary Motion

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
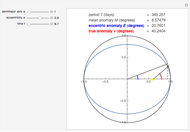
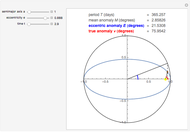
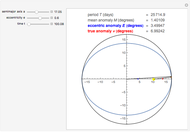
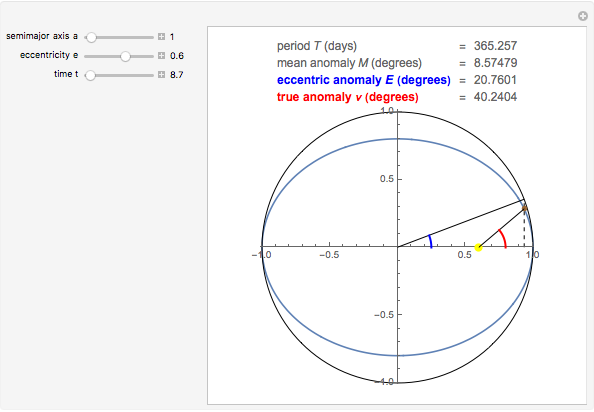
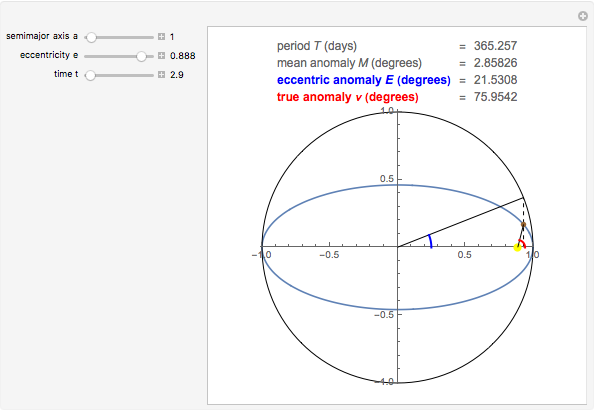
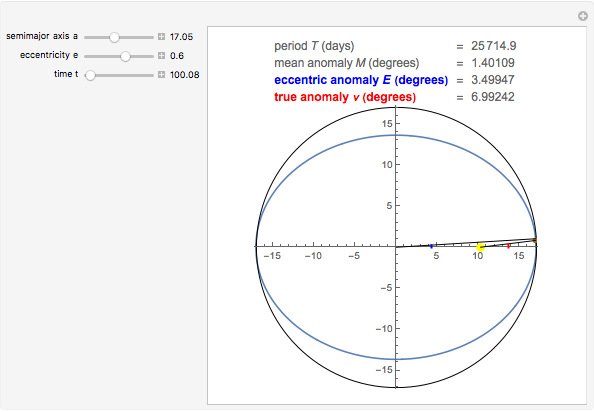
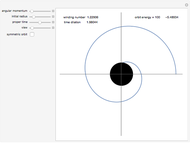
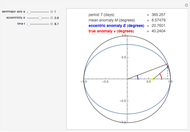
The Kepler motion of a planet (brown dot) around a star (yellow dot) follows an ellipse. Given a semimajor axis  and eccentricity
and eccentricity  , the current position of the planet at time
, the current position of the planet at time  since the perihelion passage is given by the true anomaly
since the perihelion passage is given by the true anomaly  . To determine this, we first have to calculate the eccentric anomaly
. To determine this, we first have to calculate the eccentric anomaly  from the mean anomaly
from the mean anomaly  .
.
Contributed by: Thomas Müller (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Kepler's third law gives a relation between the semimajor axis  and the period
and the period  of a planet,
of a planet,  , where
, where  is the gravitational constant and the solar mass is set equal to 1. The mean anomaly is defined as
is the gravitational constant and the solar mass is set equal to 1. The mean anomaly is defined as  , where
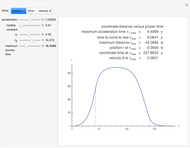
, where  is the time since the perihelion passage of the planet. To obtain the eccentric anomaly, we have to solve the Kepler equation
is the time since the perihelion passage of the planet. To obtain the eccentric anomaly, we have to solve the Kepler equation  . The true anomaly can be determined via
. The true anomaly can be determined via  . The distance between the star and the planet is given by
. The distance between the star and the planet is given by  .
.
Permanent Citation