Properties of Kerr Spacetime
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
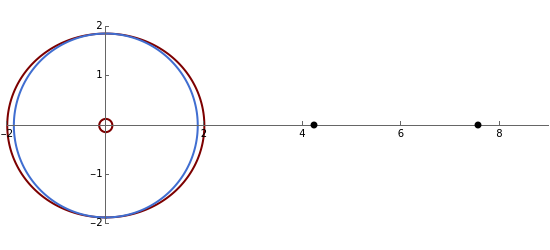
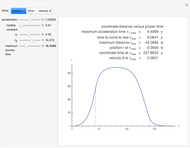
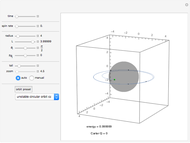
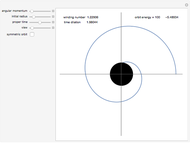
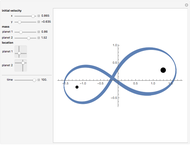
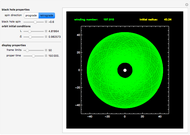
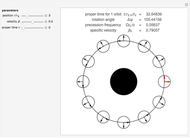
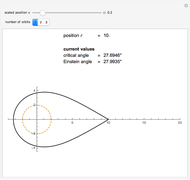
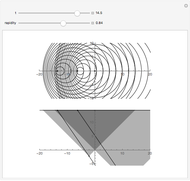
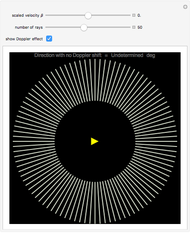
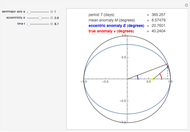
Kerr spacetime describes a rotating black hole. The line element in Boyer–Lindquist coordinates  is given by
is given by 
Contributed by: Thomas Müller (March 2011)
Open content licensed under CC BY-NC-SA
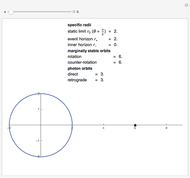
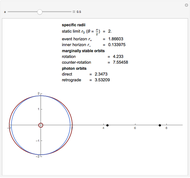
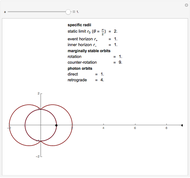
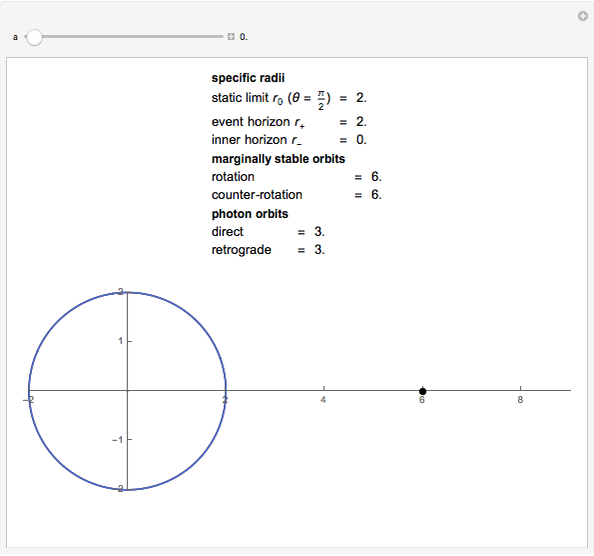
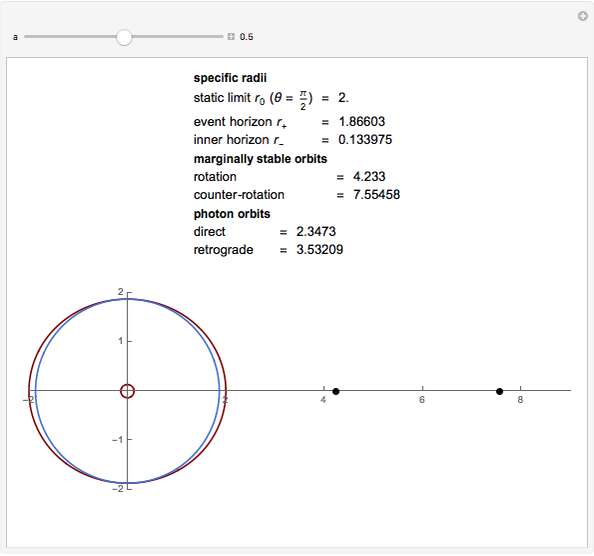
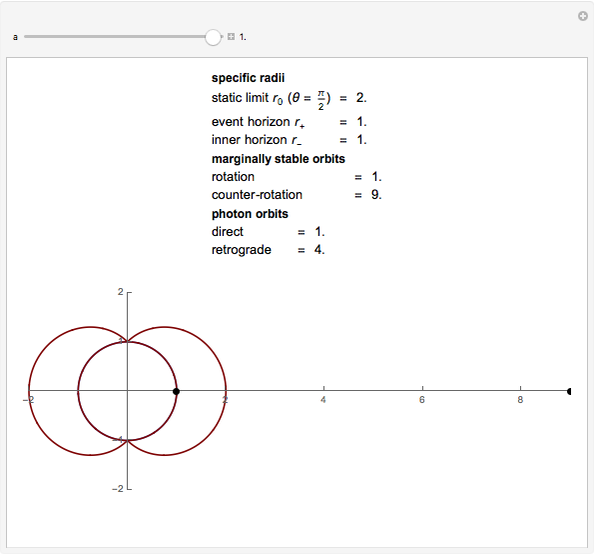
Snapshots
Details
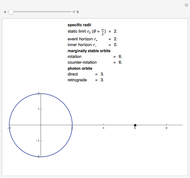
A detailed discussion of the parameters is given in:
J. M. Bardeen, W. H. Press, and S. A. Teukolsky, "Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation," The Astrophysical Journal, 178, 1972 pp. 347–369.
Permanent Citation