Area of Epicycloid and Hypocycloid
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
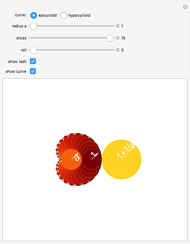
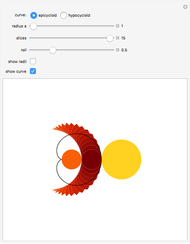
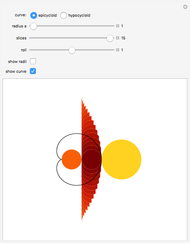
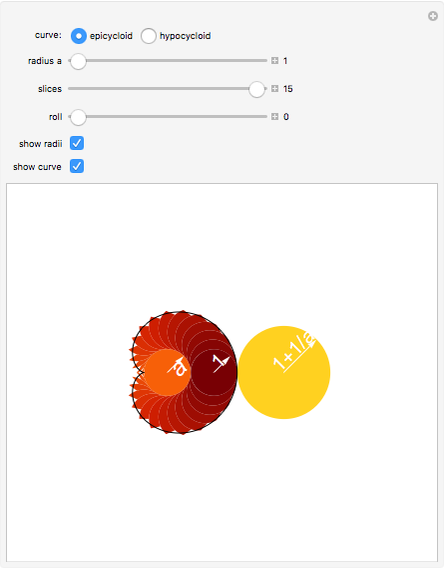
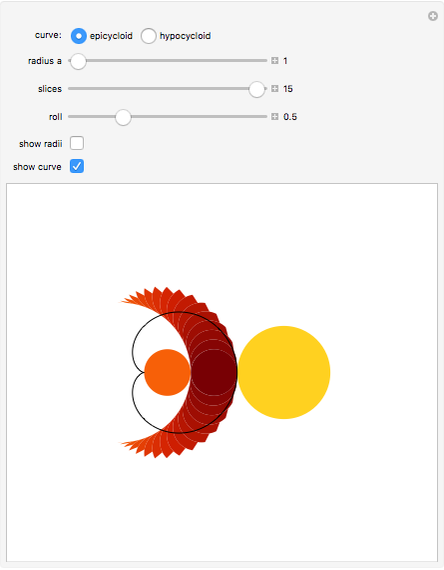
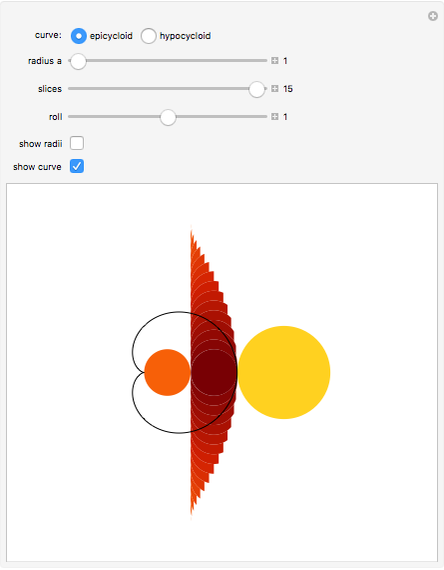
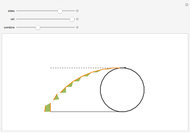
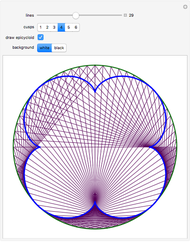
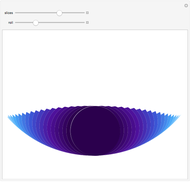
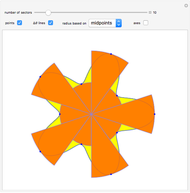
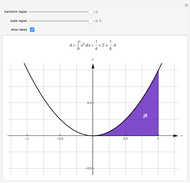
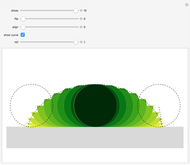
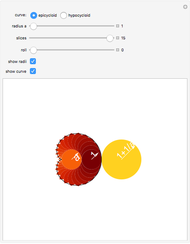
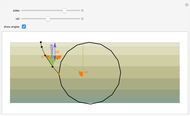
This Demonstration shows that the area under the first hump of a epicycloid is 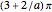 when the radii of the generating circle and greater circle are
when the radii of the generating circle and greater circle are 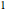 and
and  respectively. When you slide the "roll" slider, slices form a circle of radius
respectively. When you slide the "roll" slider, slices form a circle of radius 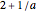 and a circular hole of radius
and a circular hole of radius 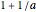 . Therefore the area is the difference of areas of the two circles. In other words,
. Therefore the area is the difference of areas of the two circles. In other words, 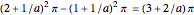 .
.
Contributed by: Okay Arik (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation