Area of Epicycloid and Hypocycloid

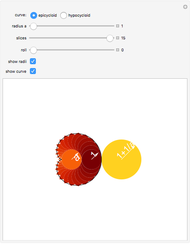
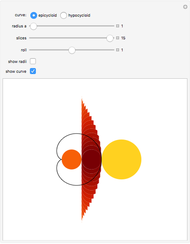
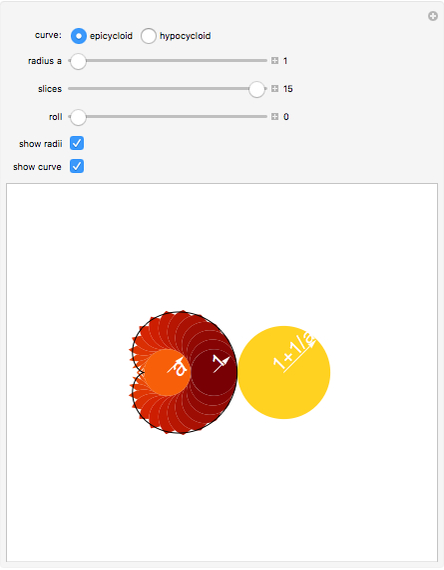
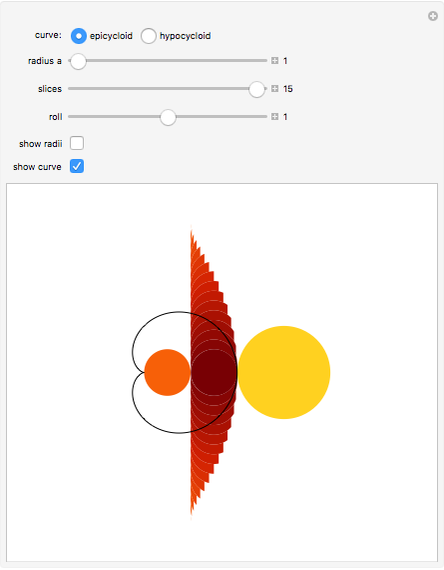
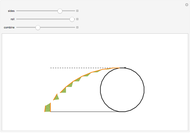
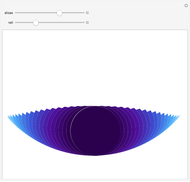
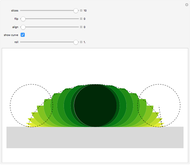
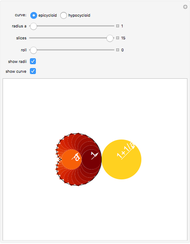
This Demonstration shows that the area under the first hump of a epicycloid is when the radii of the generating circle and greater circle are and respectively. When you slide the "roll" slider, slices form a circle of radius and a circular hole of radius . Therefore the area is the difference of areas of the two circles. In other words, .

For the hypocycloid, the same result holds with negative.

As the number of slices goes to infinity, the dark figure approaches a region bounded by a perfect epicycloid or hypocycloid.