Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Areas of Squares from the Pedals of a Triangle

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

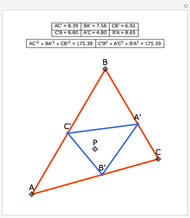
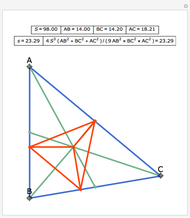
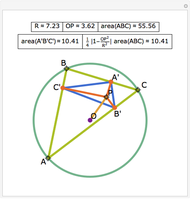
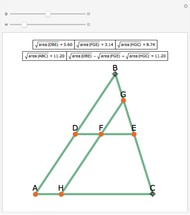
For a triangle and a point , let , and be the projections of the point to the opposite sides. Then is called the pedal triangle of .

[more]

Construct squares on the segments , , , , and and color them alternately blue and green. Bottema's theorem states that the sum of the areas of the three squares of one color equals the sum of the squares of the other color.

Drag to vary the shape of .

[less]

Contributed by: Tomas Garza (January 2020)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Reference

[1] Z. Cerin, "Rings of Squares Around Orthologic Triangles," Forum Geometricorum, 9, 2009 pp. 57–80. forumgeom.fau.edu/FG2009volume9/FG200906.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send