A Concurrency from Six Pedal Points

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
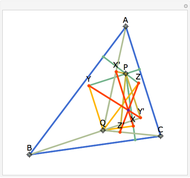
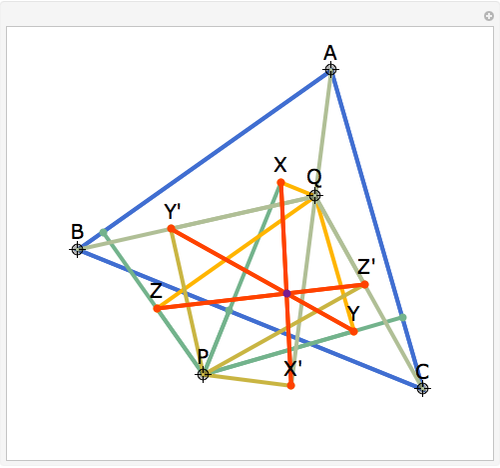
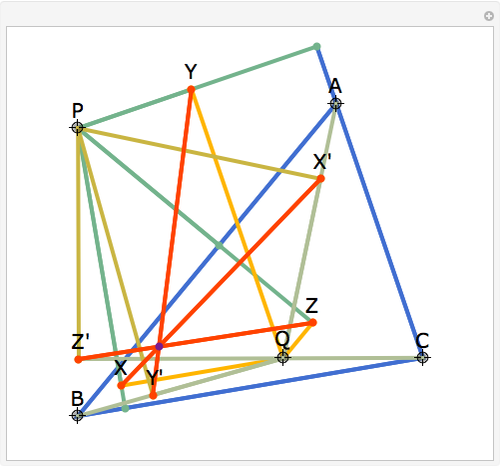
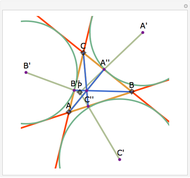
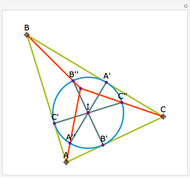
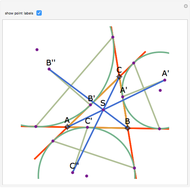
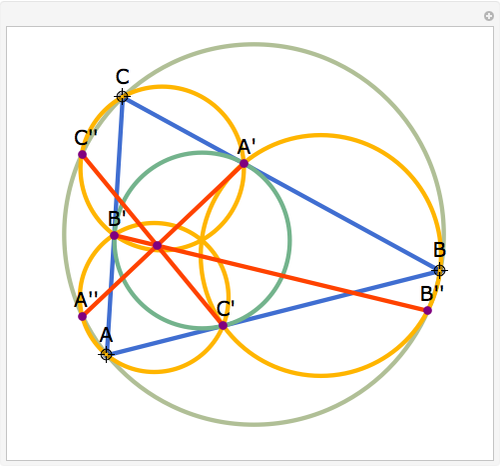
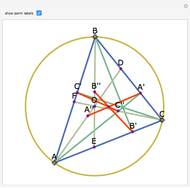
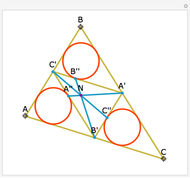
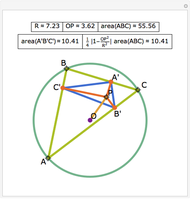
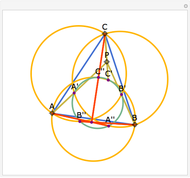
Let ABC be a triangle and P and Q be two other points. Drop perpendiculars from P to the three sides of ABC. Let X, Y, and Z be the feet of the perpendiculars (pedals) of Q on the three perpendiculars. Let X', Y', and Z' be the pedals of P on AQ, BQ, and CQ. Then XX', YY", and ZZ' are concurrent.
Contributed by: Jay Warendorff (September 2008)
After work by: Darij Grinberg
Open content licensed under CC BY-NC-SA
Snapshots
Details
The theorem is contained in "The Theorem on the Six Pedals", available on Darij Grinberg's home page.
Permanent Citation
"A Concurrency from Six Pedal Points"
http://demonstrations.wolfram.com/AConcurrencyFromSixPedalPoints/
Wolfram Demonstrations Project
Published: September 10 2008