Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Pedal Triangles of Isogonal Conjugates

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

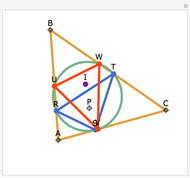
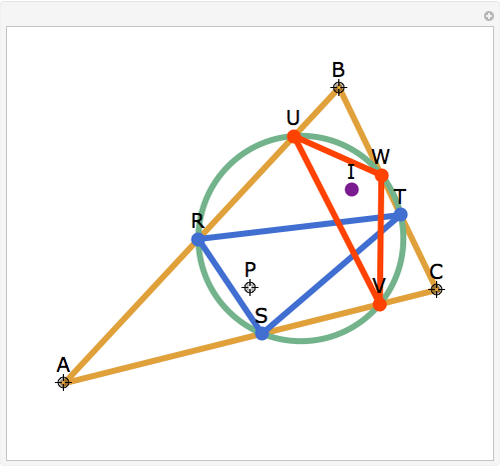
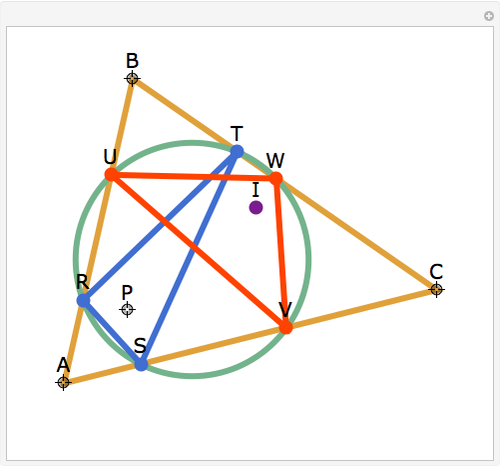
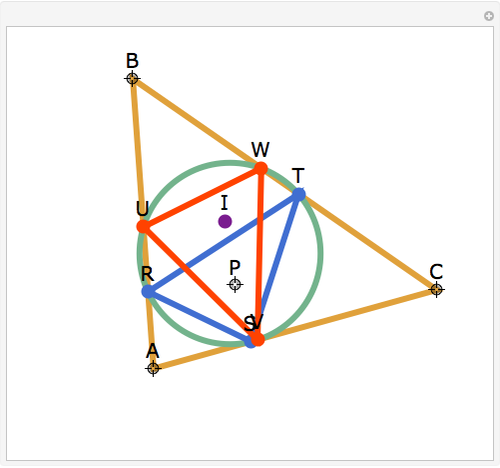
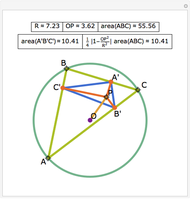
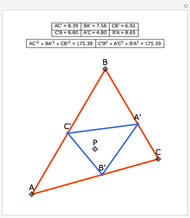
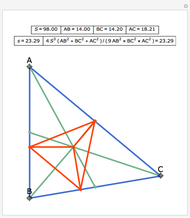
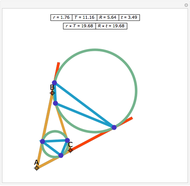
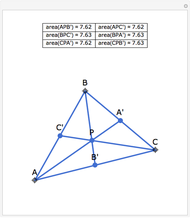
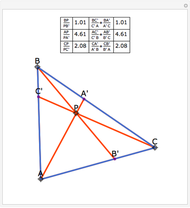
Let ABC be a triangle and P be a point. The reflections of the three lines AP, BP, and CP in the angle bisectors at A, B, and C meet in a point I, called the isogonal conjugate of P.

[more]

The feet of the perpendiculars from P to the sides of triangle ABC form the pedal triangle of P, RST. Similarly, let the pedal triangle of I be UVW.

Then R, S, T, U, V, W all lie on a circle.

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The theorem is stated in:

N. A. Court, "Isogonal Conjugate Points for a Triangle," The Mathematical Gazette, 36(317), 1952 pp. 167–170.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send