Asymmetric Simple Exclusion Processes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
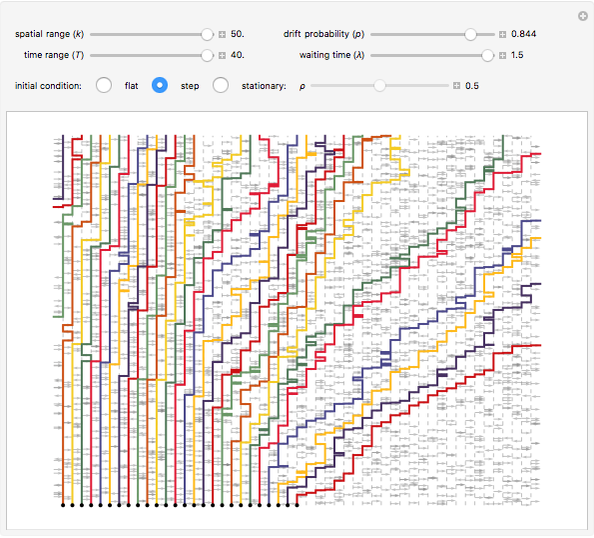
This Demonstration shows the evolution of a partially asymmetric simple exclusion process (PASEP) on the integer lattice  . In PASEP, a particle waits an exponential amount of time, then moves to the right with probability
. In PASEP, a particle waits an exponential amount of time, then moves to the right with probability  or to the left with probability
or to the left with probability  , unless the site is occupied. In the case
, unless the site is occupied. In the case  , the dynamic is totally asymmetric, and the process is known as a totally asymmetric simple exclusion process (TASEP).
, the dynamic is totally asymmetric, and the process is known as a totally asymmetric simple exclusion process (TASEP).
Contributed by: Alessandra Occelli and Lorenzo Dello Schiavo (August 2018)
Open content licensed under CC BY-NC-SA
Details
The evolution of the asymmetric simple exclusion process (ASEP) is represented on the  -plane using a graphical construction: in each column the arrows
-plane using a graphical construction: in each column the arrows  and
and  are generated as independent Poisson processes of density
are generated as independent Poisson processes of density  , and the direction of the arrows is given by a random variable of Bernoulli distribution with parameter
, and the direction of the arrows is given by a random variable of Bernoulli distribution with parameter  .
.
Once the initial condition is given, the trajectories of the process are uniquely determined by arrow configurations. The trajectory of a particle is represented by a continuous line. Every time a particle meets an arrow, it changes its position according to the direction of the arrow, if the site indicated by the arrow is empty. For this reason, lines never cross, and the order of the particles is preserved by the evolution.
The trajectory of a particle exiting and then reentering the bulk is represented in the same color.
Snapshot 1: flat initial conditions
Snapshot 2: step initial conditions
Snapshot 3: stationary initial conditions
Reference
[1] T. M. Liggett, Interacting Particle Systems, New York: Springer-Verlag, 1985.
Snapshots
Permanent Citation