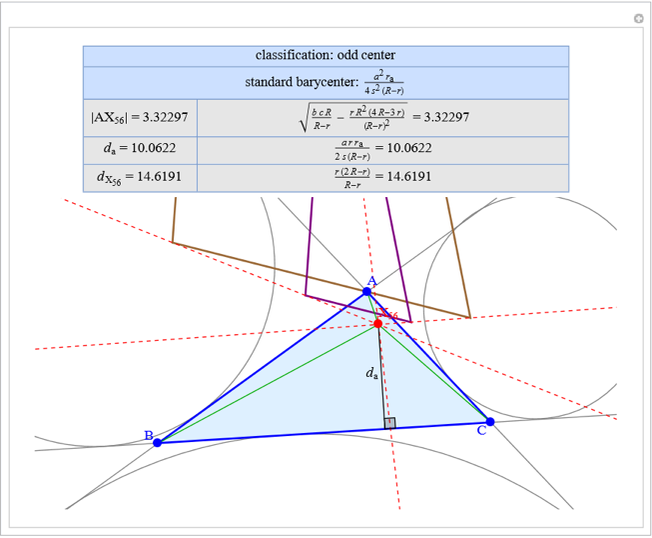
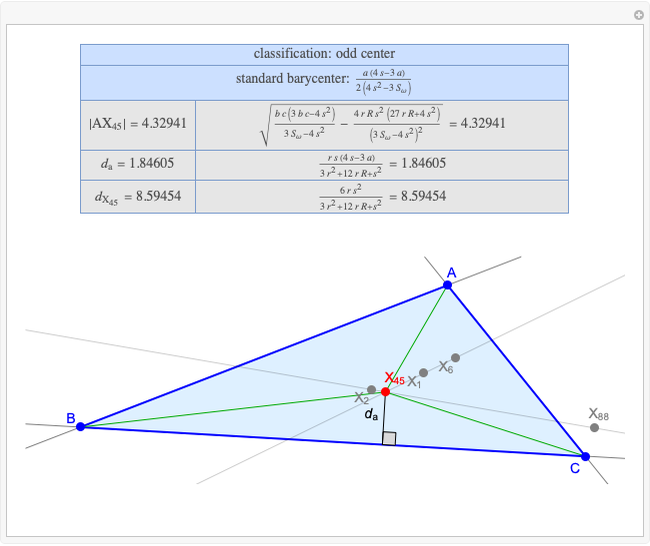
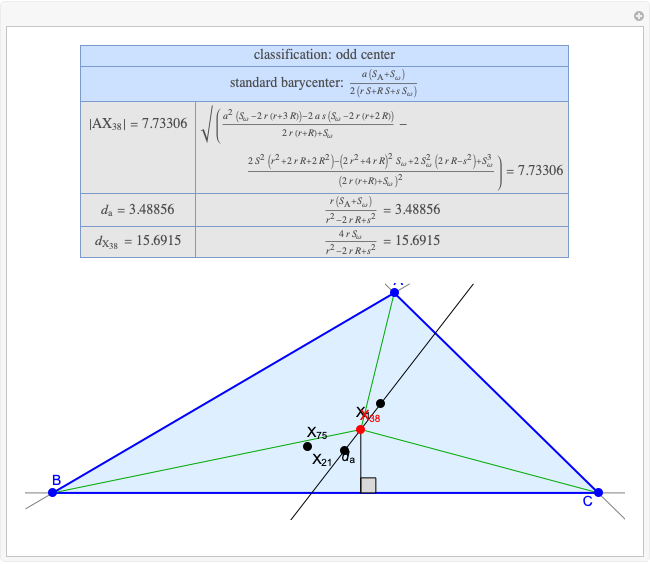
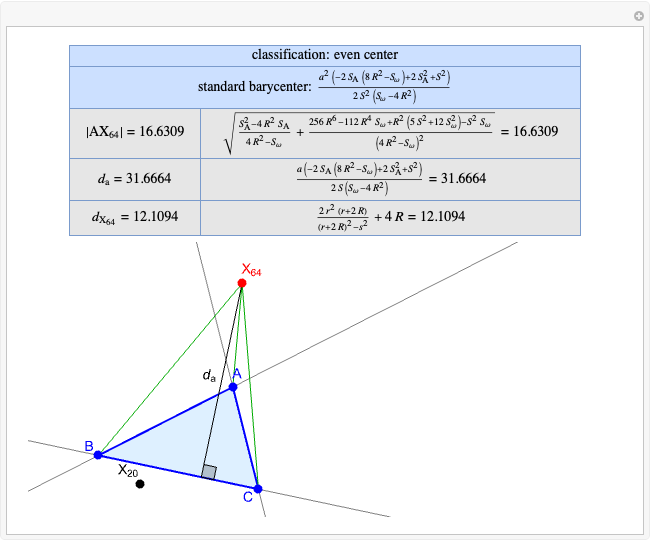
Basic Parameters of the Kimberling Center X(52)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
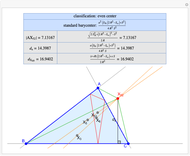
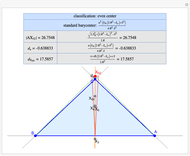
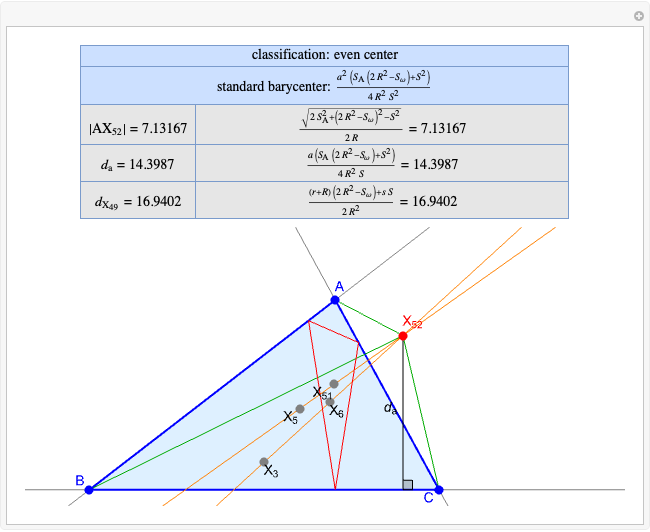
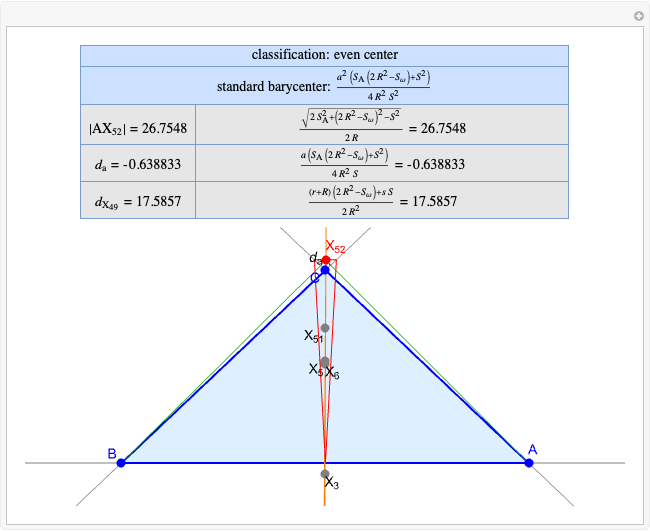
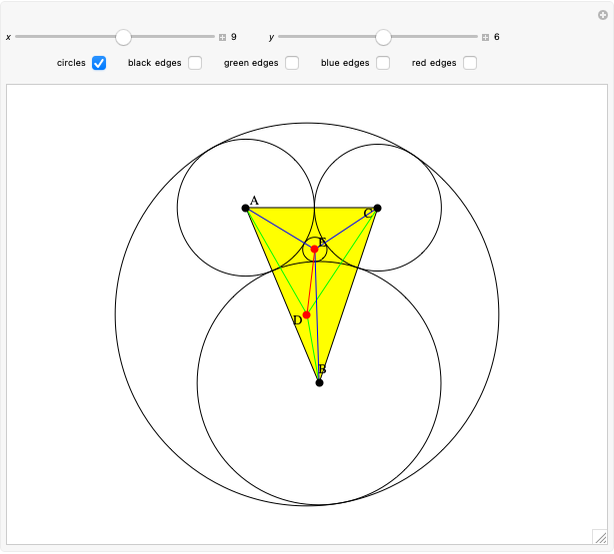
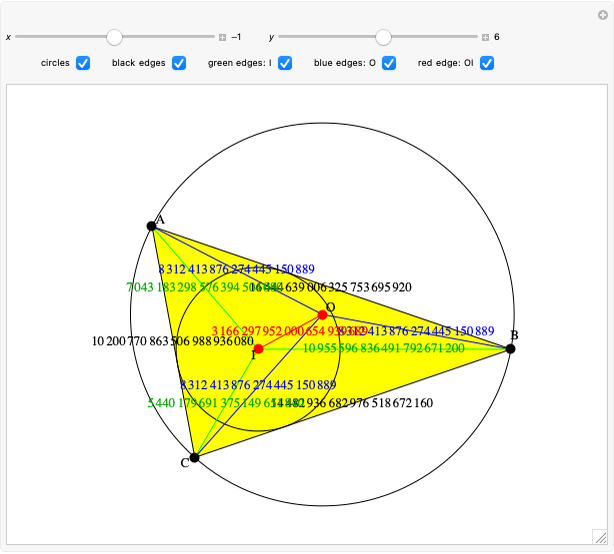
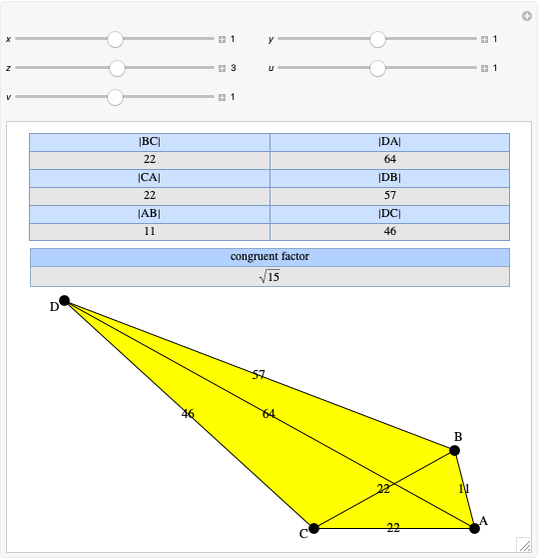
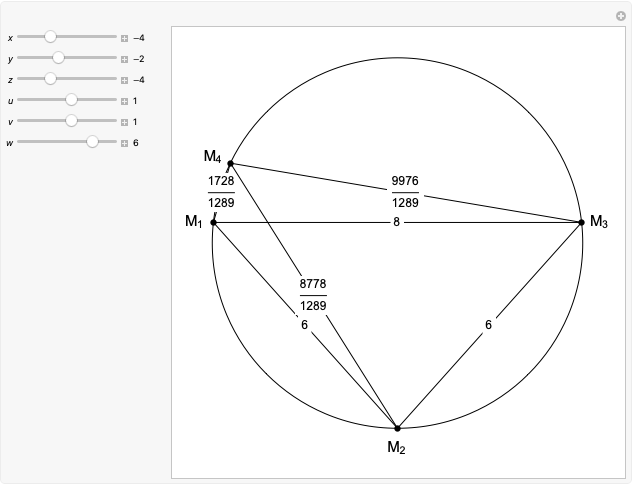
Given a triangle  , the Kimberling center
, the Kimberling center  is the orthocenter of the orthic triangle (shown in red) [1].
is the orthocenter of the orthic triangle (shown in red) [1].
Contributed by: Minh Trinh Xuan (August 25)
Open content licensed under CC BY-NC-SA
Details
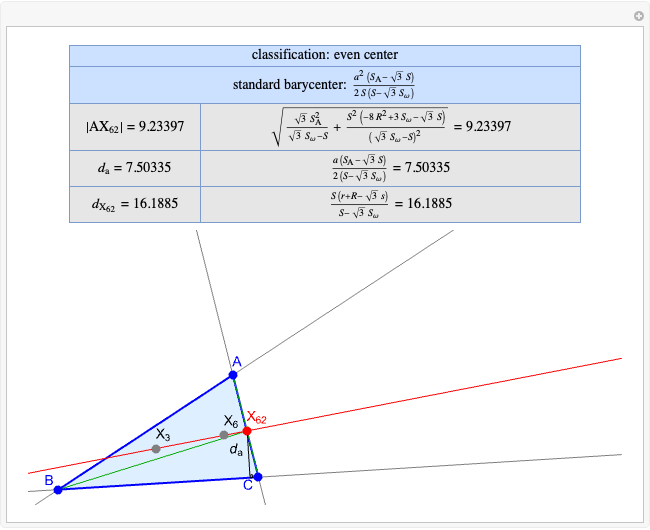
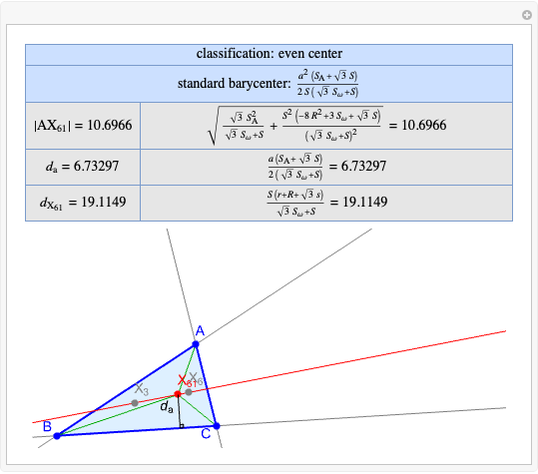
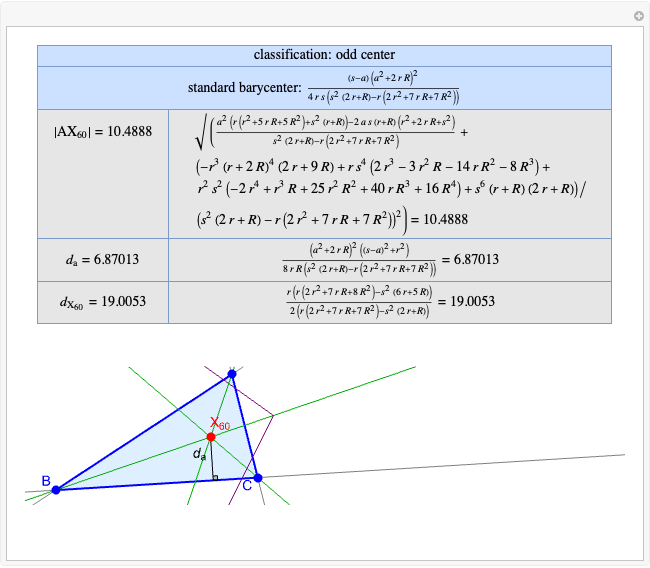
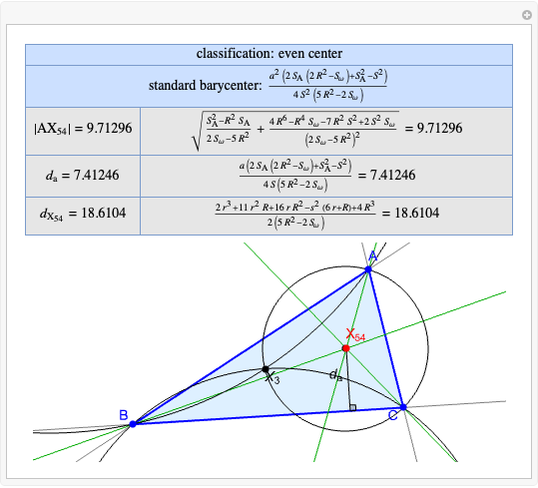
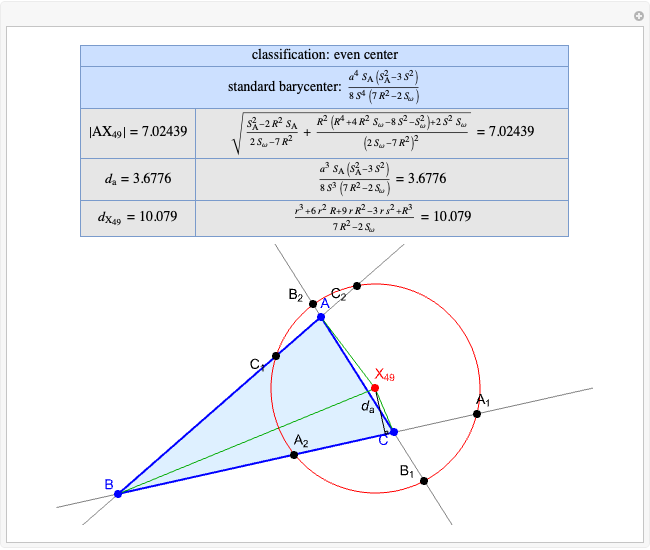
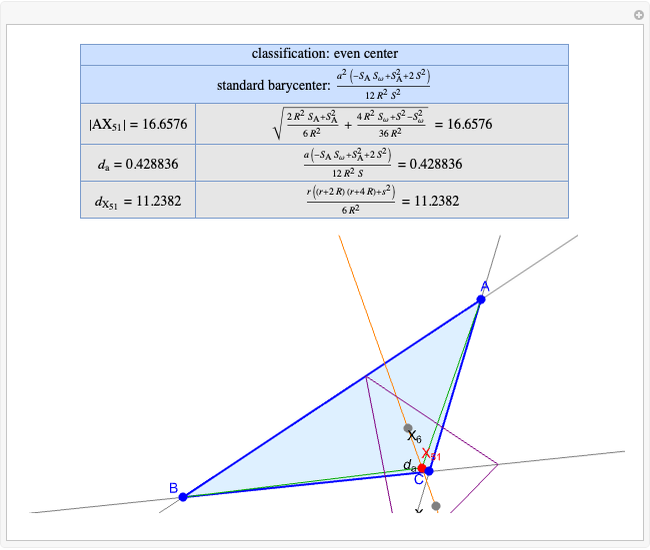
A triangle center is said to be even when its barycentric coordinates can be expressed as a function of three variables  ,
,  ,
,  that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid
that all occur with even exponents. If the center of a triangle has constant barycentric coordinates, it is called a neutral center (the centroid  is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
is the only neutral center). A triangle center is said to be odd if it is neither even nor neutral.
Standard barycentric coordinates of a point with respect to a reference triangle have a sum of 1.
Reference
[1] C. Kimberling. "Encyclopedia of Triangle Centers." (Jun 1, 2023) faculty.evansville.edu/ck6/encyclopedia.
Snapshots
Permanent Citation