Bending and Stretching of an Elastic L-Beam

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
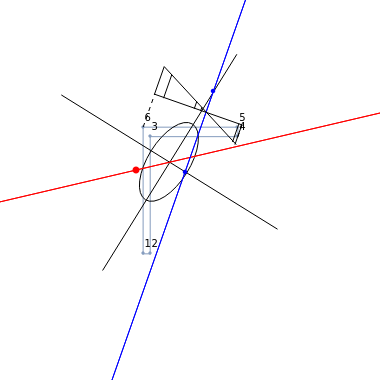
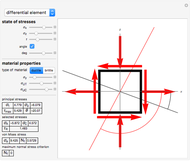
The normal stresses (a.k.a. longitudinal stresses) in an elastic beam with an L-shaped cross section loaded by bending moments and by a normal force are computed by the generalized Navier's formula.
[more]
Contributed by: Maurizio Brocato (June 2020)
Open content licensed under CC BY-NC-SA
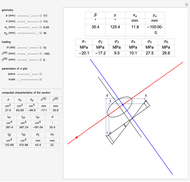
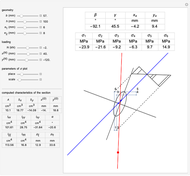
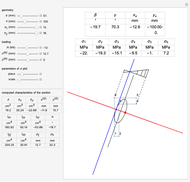
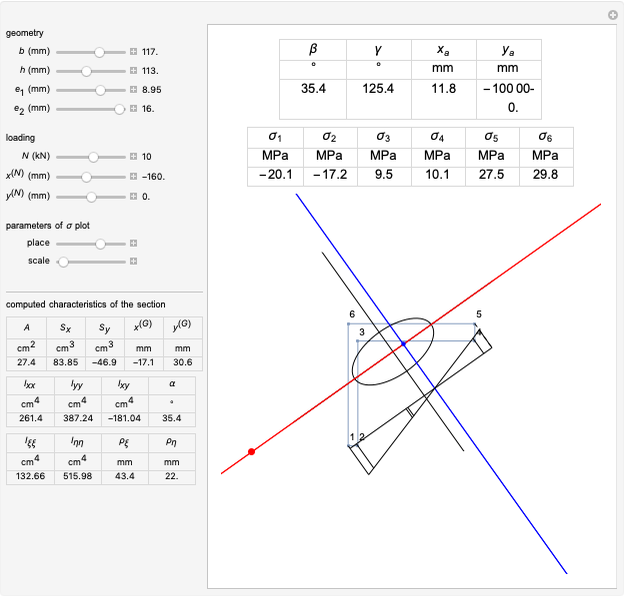
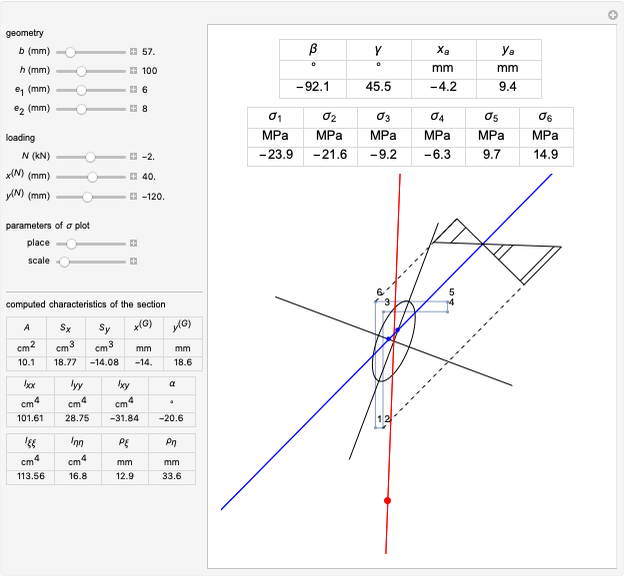
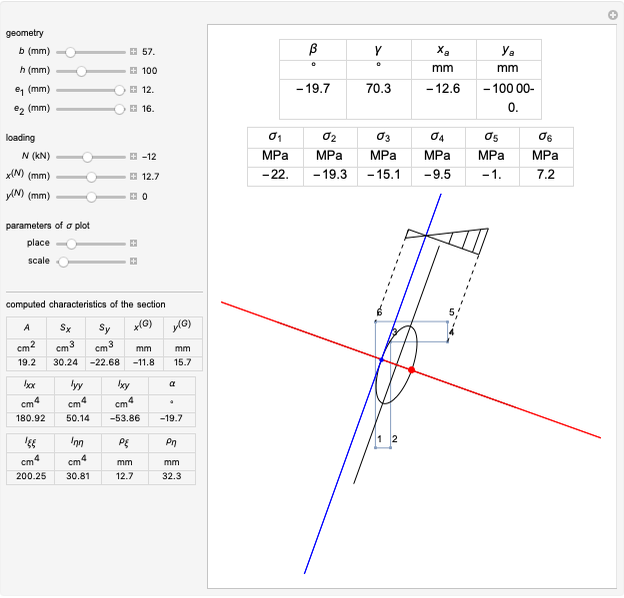
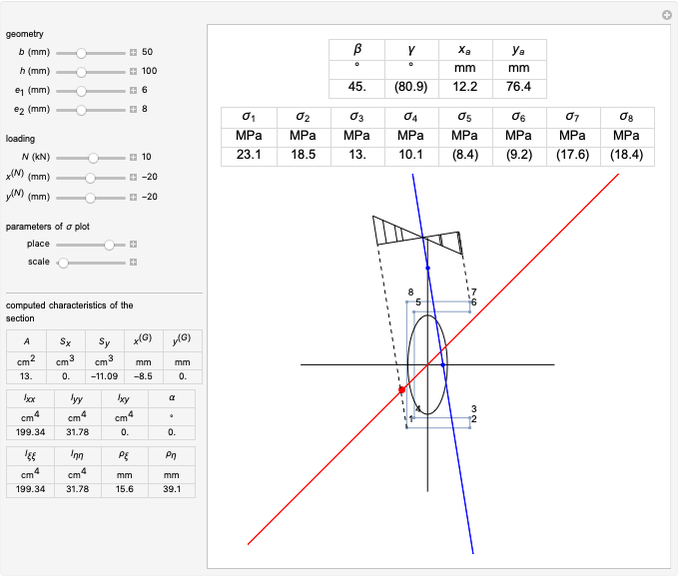
Snapshots
Details
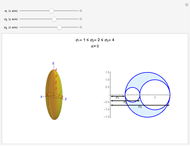
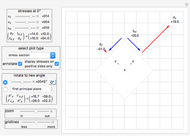
The generalized Navier's solution for bending and stretching depends on the geometry of the cross section of the beam, on the position of the applied normal force and on its intensity. The point at the intersection of the axis of the normal force with the plane of the cross section is called the center of pressure. The line joining it with the barycenter of the cross section is called the axis of loading. Pure bending corresponds to the limit of a null normal force applied at an infinite distance; pure tension or compression corresponds to a normal force applied on the barycenter (a.k.a. centroid).
The solution in terms of normal stresses is an affine field, characterized by a neutral axis (where the field is null). The neutral axis and the center of pressure are related by an anti-polarity property depending on the ellipse of inertia: the neutral axis is parallel to the tangent to the ellipse where it intersects with the axis of loading and its distance from the barycenter is inversely proportional to that of the same point from the center of pressure.
Details are given in textbooks on the theory of elasticity and structural mechanics, including elements of the theory of elastic beams, for example [1].
The symbols of the input parameters have the following meanings:
 = width or length of the flange
= width or length of the flange
 = height or length of the web
= height or length of the web
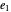 = thickness of the web
= thickness of the web
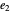 = thickness of the flange
= thickness of the flange
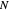 = normal force
= normal force
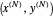 = coordinates of the center of pressure (red point)
= coordinates of the center of pressure (red point)
The parameters of the 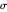 plot allow you to displace it along the direction of the neutral axis and to set its amplitude. The computed geometric characteristics of the section, displayed under the controls, are:
plot allow you to displace it along the direction of the neutral axis and to set its amplitude. The computed geometric characteristics of the section, displayed under the controls, are:
 = surface area
= surface area
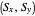 = static moments (a.k.a. first moments of area)
= static moments (a.k.a. first moments of area)
(x(G),y(G)) = coordinates of the barycenter
(Ixx,Iyy,Ixy) = inertial moments (a.k.a. second moments of area)
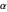 = angle between the first principal axis of inertia and the
= angle between the first principal axis of inertia and the 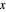 axis
axis
(Iξξ,Iηη) = principal inertial moments
(ρξ,ρη) = radii of gyration
The results displayed under the image are:
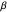 = angle between the axis of bending and the
= angle between the axis of bending and the 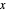 axis
axis
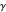 = angle between the neutral axis and the
= angle between the neutral axis and the 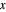 axis
axis
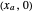 and
and 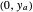 = intersections of the neutral axis with the principal coordinate axes (blue points)
= intersections of the neutral axis with the principal coordinate axes (blue points)
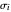 = stress at point
= stress at point  on the perimeter according to the numbering displayed in the figure (shown by a segment in the
on the perimeter according to the numbering displayed in the figure (shown by a segment in the 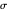 plot)
plot)
Reference
[1] M. Brocato, Cours de mécanique des structures. Volume 1. Poutres élastiques, Paris: Presses des Ponts, forthcoming.
Permanent Citation