Navier Solution for a Singularly Loaded Kirchhoff Rectangular Plate

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
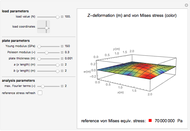
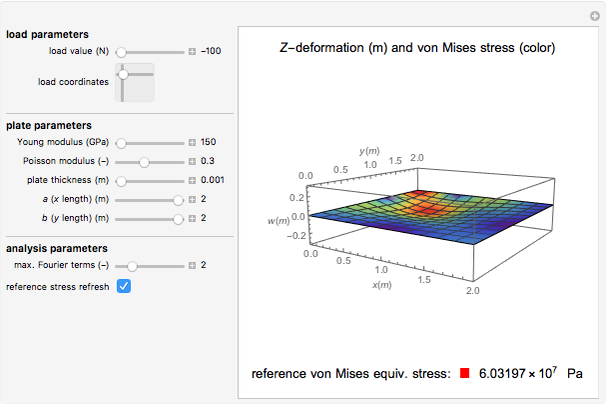
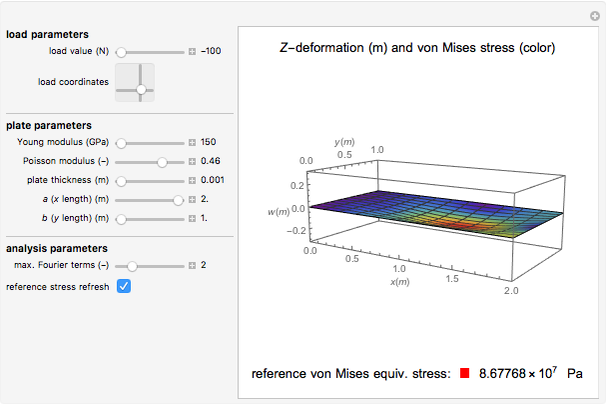
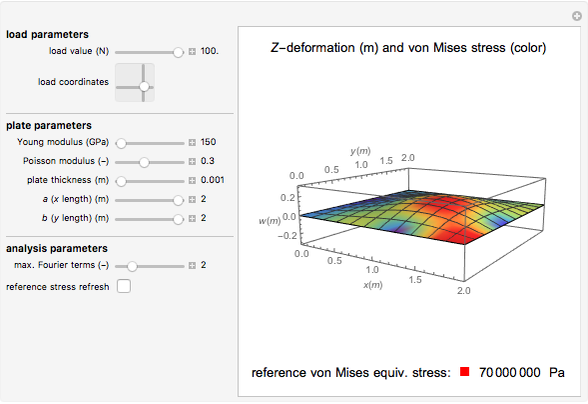
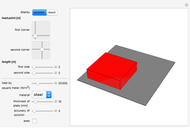
This Demonstration illustrates the approximate Navier solution for the bending and stress analysis of a simply supported Kirchhoff rectangular plate subject to a concentrated singular load applied at given coordinates. The deformation of the middle surface is represented on a 3D plot, colored according to its von Mises equivalent stress.
Contributed by: Jorge García Tíscar (September 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Start from the classical equation for pure bending of a simply supported Kirchhoff plate with dimensions 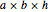 , Young modulus
, Young modulus  , and Poisson modulus
, and Poisson modulus  subject to a load
subject to a load  :
:
 (flexural rigidity).
(flexural rigidity).
Assume a general sinusoidal load of the form
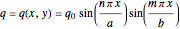 .
.
Assume a solution for the deformation of the form
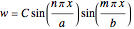 .
.
Consider the boundary conditions of the simply supported plate:
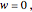
 at
at 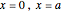 ,
,
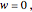
 at
at 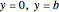 .
.
Then you get the following general solution:
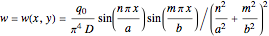 .
.
In this case, the load is a singular one of value 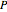 applied at coordinates
applied at coordinates 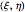 :
:
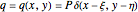 .
.
Follow Navier's procedure by expanding the load as a Fourier series:
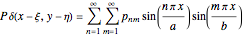 .
.
Solving for  (using orthogonality) you get
(using orthogonality) you get
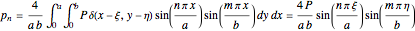 .
.
Introducing the coefficients in the prior general solution and applying the principle of superposition, you can derive a general expression for the deformation under unitary load ( ) applied at coordinates
) applied at coordinates 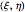 :
:
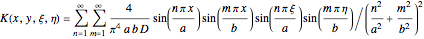 .
.
You can then calculate the deformation 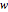 , multiplying by the load value
, multiplying by the load value 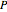 :
:
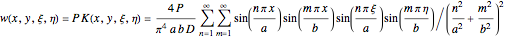 .
.
Now you can compute the stresses at the top of the plate  ), following the classic theory of Kirchhoff plates:
), following the classic theory of Kirchhoff plates:
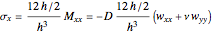 ,
,
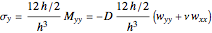 ,
,
 .
.
You can then find the two principal stresses (Kirchhoff theory assumes plane stress):
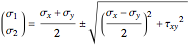
Finally, you can obtain the von Mises equivalent stress:
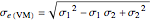
Reference
[1] S. P. Timoshenko, Theory of Plates and Shells, New York: McGraw–Hill, 1959.
Permanent Citation