Bicycle Wheels Using Curves of Constant Width

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
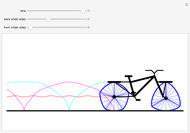
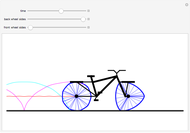
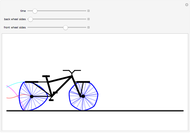
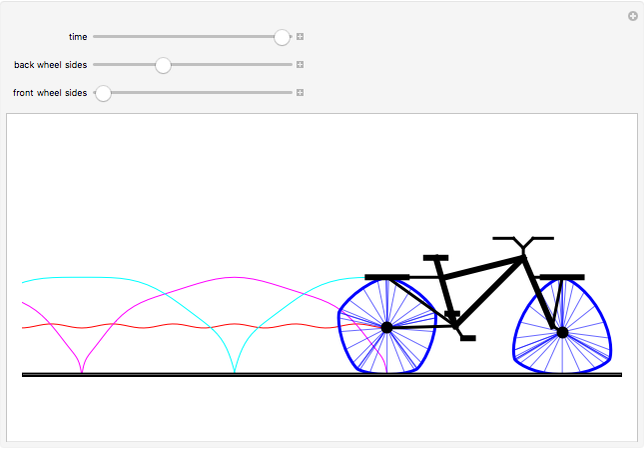
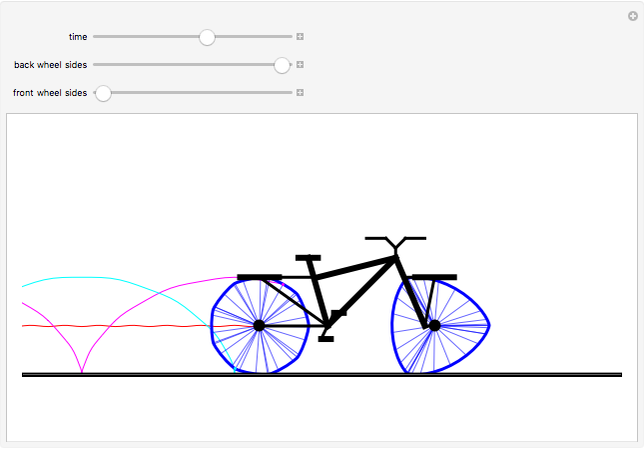
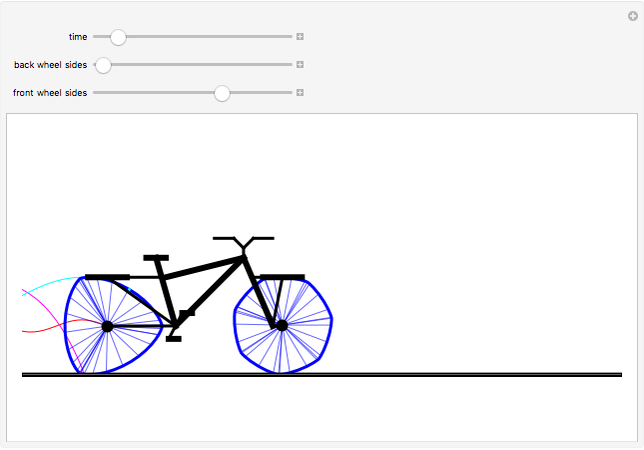
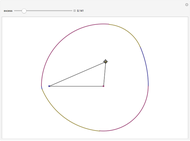
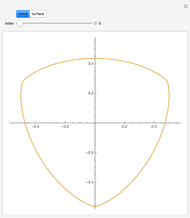
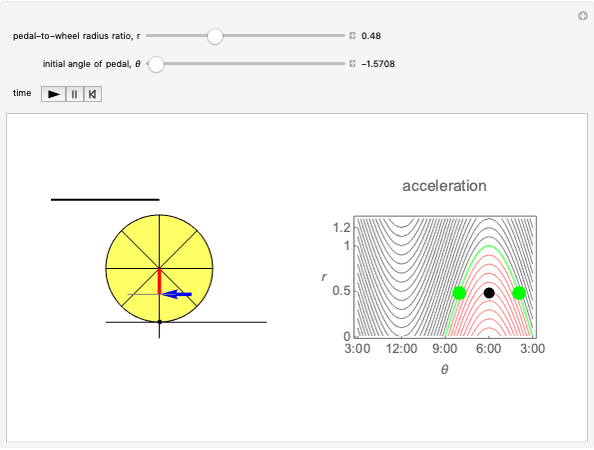
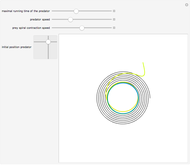
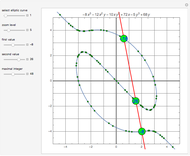
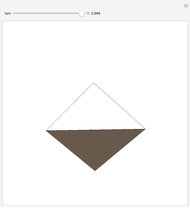
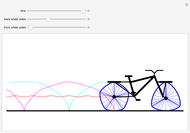
Curves of constant width are planar curves that maintain the same width and height when rotated. Such curves can be created using any odd number of sides between three and infinity, and include Reuleaux triangles and circles. When rolled as wheels of a bicycle, curves of constant width provide a uniform ride as long as the rider is supported by the top of each wheel rather than by the center, as in traditional bicycles. The only known physical bicycle using curves of constant width was created by Guan Baihua in China. Curves are shown to trace the locations of two points on the back wheel as well as the center of the back wheel over time.
Contributed by: Robert Young (January 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The idea is from [1]. More information about curves of constant width can be found in [2].
References
[1] "Reuleaux Wheeled Bicycle." (Jan 6, 2014) britton.disted.camosun.bc.ca/reuleaux_bike/reuleaux_bike.html.
[2] J. Bryant and C. Sangwin, How Round is Your Circle?, Princeton, NJ: Princeton University Press, 2011.
[3] triangle bicycle
Permanent Citation
"Bicycle Wheels Using Curves of Constant Width"
http://demonstrations.wolfram.com/BicycleWheelsUsingCurvesOfConstantWidth/
Wolfram Demonstrations Project
Published: January 7 2014