Bisecting the Area and Perimeter of a Triangle

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
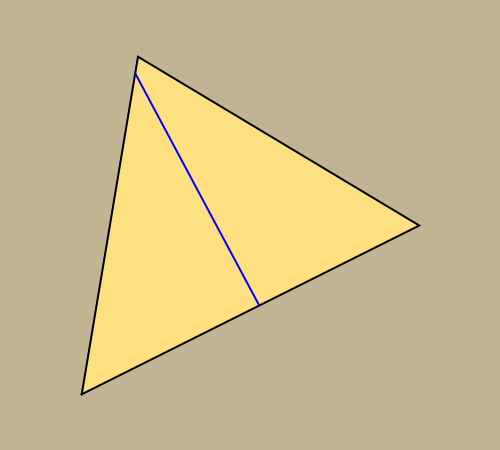
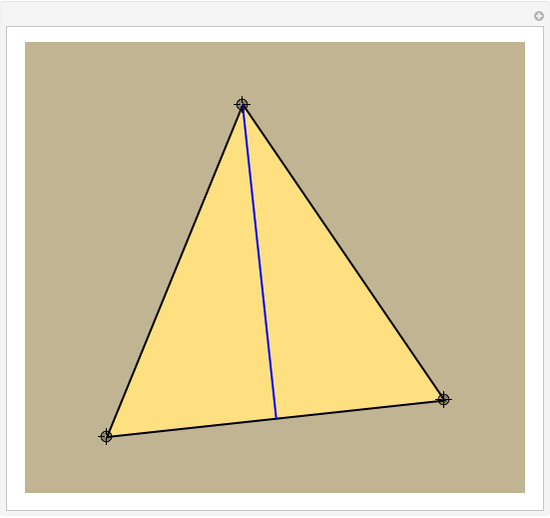
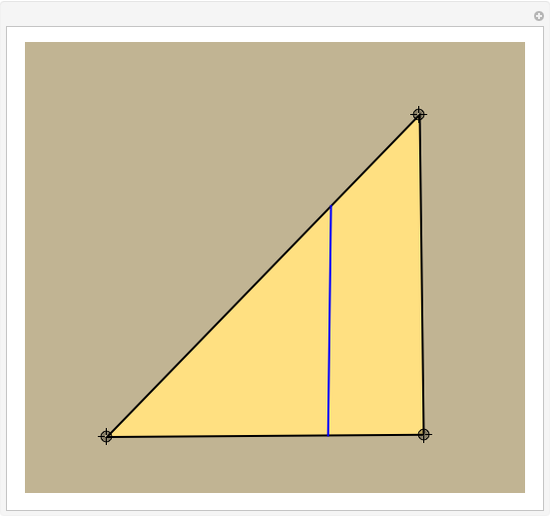
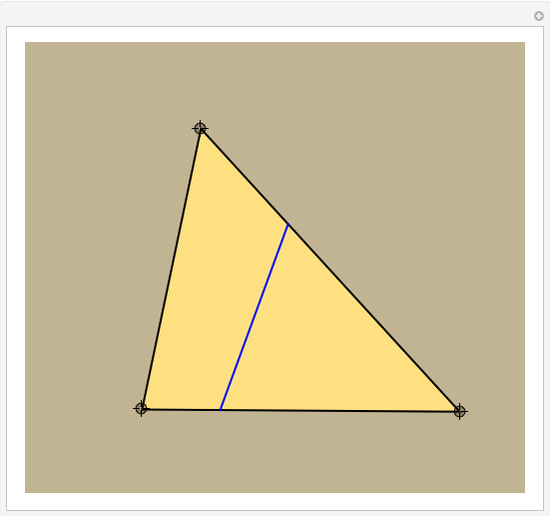
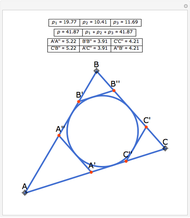
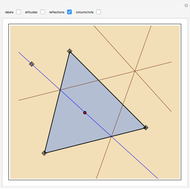
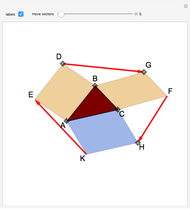
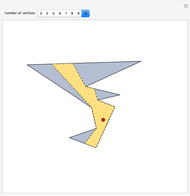
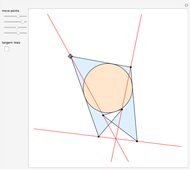
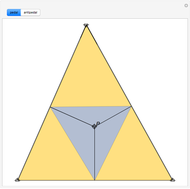
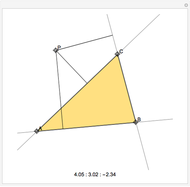
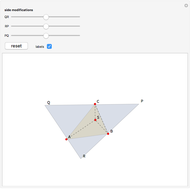
This Demonstration constructs a line that divides a triangle into two figures of equal area and equal perimeter.
Contributed by: Jaime Rangel-Mondragon (July 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
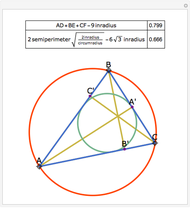
Some fascinating results motivated me to make this Demonstration. For instance, any line through the incenter of a triangle (where the three internal angle bisectors meet) that divides its area in half also divides its perimeter in half; conversely, any line through the incenter that divides the perimeter of the triangle in half also divides its area in half. More generally, we have Haider's theorem: for any triangle 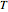 and any line
and any line 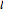 ,
, 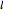 divides the area and perimeter of
divides the area and perimeter of 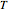 in the same ratio if and only if it passes through the incenter of
in the same ratio if and only if it passes through the incenter of 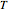 .
.
One of the difficult problems designed to eliminate many targeted applicants in entrance examinations to the Mekh-Mat at Moscow State University during the 1970s and 1980s was to draw a straight line that bisects the area and perimeter of a triangle. Showing the existence of such a line is quite easy; constructing that line is much harder.
References
[1] S. Campo Ruiz. "Solución Problema 138." (Jul 9, 2013) www.aloj.us.es/rbarroso/trianguloscabri/sol/sol138sat.htm.
[2] Math Central. "Problem of the Month, Solution for April 2012." (Jul 9, 2013) mathcentral.uregina.ca/mp/previous2011/apr12sol.php.
[3] I. Vardi. "Mekh-Mat Entrance Examination Problems." (Jul 9, 2013) www.lix.polytechnique.fr/Labo/Ilan.Vardi/mekh-mat.html.
Permanent Citation
"Bisecting the Area and Perimeter of a Triangle"
http://demonstrations.wolfram.com/BisectingTheAreaAndPerimeterOfATriangle/
Wolfram Demonstrations Project
Published: July 10 2013