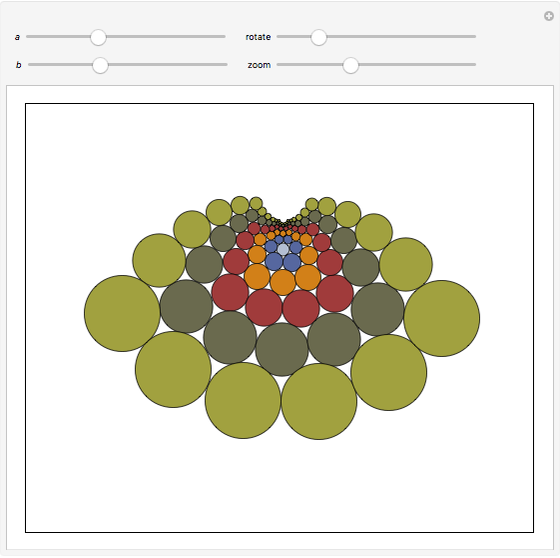
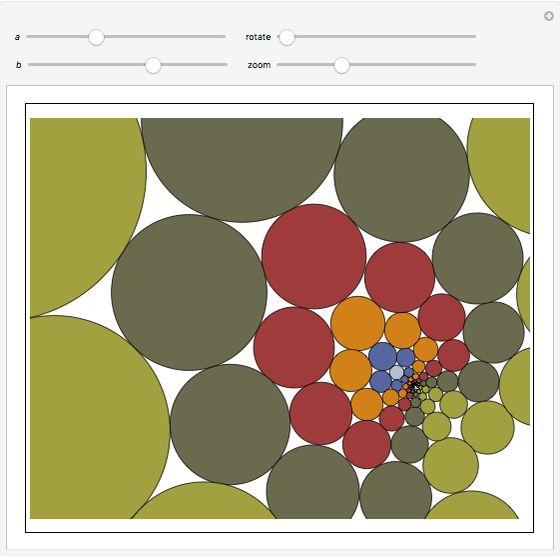
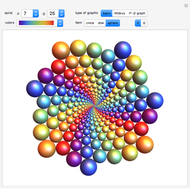
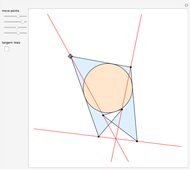
Doyle spirals are stunning patterns made of tangent circles, each of which touches six others. The method of generating these and many other patterns started with Peter Doyle's now-historical observation: suppose and are positive real numbers. Then six circles of successive radii close up exactly when placed tangent to one another around a circle of radius 1.