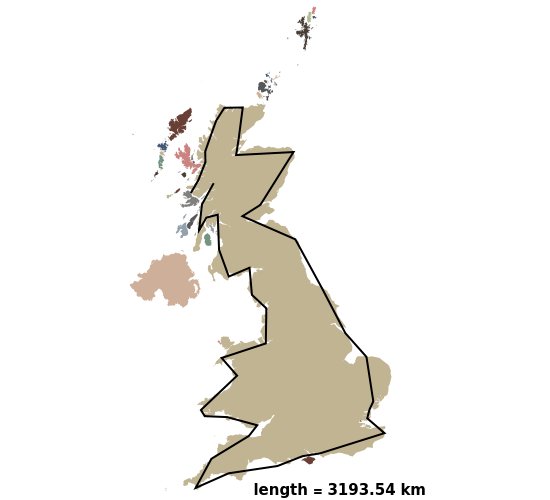
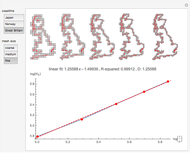
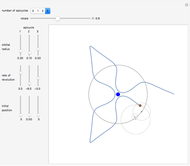
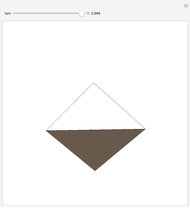
This Demonstration examines the coastline paradox, studied by Benoit Mandelbrot (1924–2010) in his influential 1967 short paper "How Long Is the Coast of Britain?" [3]. The smaller the length of the measuring stick, the longer the length of the coast appears, so that in the limit the coast of the island of Great Britain is of infinite length! Starting from an empirical law obtained previously by Richardson, Mandelbrot introduced the idea of "fractals", concluding that it is meaningless to talk about the length of a coastline and proposing a generalization of the concept of fractal dimension to measure the degree of roughness involved in such measurements.