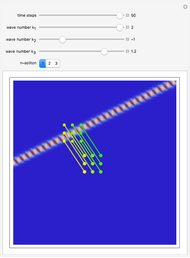
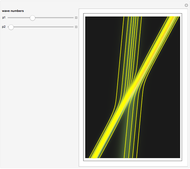
Blip Solitons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
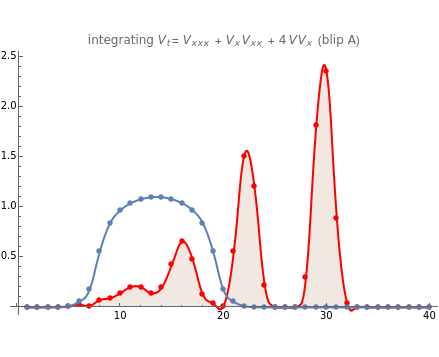
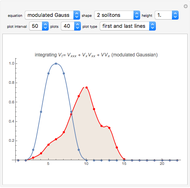
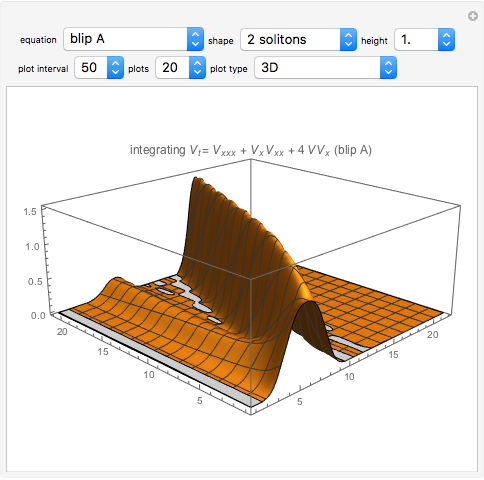
Integration of two simultaneous partial differential equations (PDEs) converts initial disturbances (the points on the blue line) into stable solitonic "blips" (the red points) with speeds related to heights. One, two, or more distinct blips are generated from different initial conditions. The filled red line attempts quadratic interpolation of the red points, but sometimes disappears or becomes negative because the points are on a spiky function. Both equations give similar results. They are related to a third "modulated Gaussian" equation that is shown but that requires further research.
[more]
Contributed by: Roger Beresford (August 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Solitonic behavior often arises when a conservative functional relationship such as  is solved. The two-blip equations have
is solved. The two-blip equations have  ,
,  , where
, where  is an arbitrary multiplier; this simplifies after differentiation to
is an arbitrary multiplier; this simplifies after differentiation to  . As both equations conserve the same properties (differing only by the scaling factor
. As both equations conserve the same properties (differing only by the scaling factor  ) they can be adjusted to give similar results at high values of
) they can be adjusted to give similar results at high values of  . They were discovered as a stable variation on a third equation that was expected to have solitonic "modulated Gaussian" pulses. (This equation shows the development of modulations in the last snapshot).
. They were discovered as a stable variation on a third equation that was expected to have solitonic "modulated Gaussian" pulses. (This equation shows the development of modulations in the last snapshot).
The integration uses a very simple "forward Euler" procedure. Equispaced values of the initial function  are labeled
are labeled  ,
,  ,
,  ,
,  , and
, and  . The value of
. The value of  after one time step is stored in
after one time step is stored in  , using
, using  and so on for the derivatives;
and so on for the derivatives;  ,
,  ,
,  , and
, and  are then cycled left and a new value (allowing for wraparound) found for
are then cycled left and a new value (allowing for wraparound) found for  . At the end of a cycle
. At the end of a cycle  is replaced by
is replaced by  ; a copy is saved at intervals for later output. The integration step length is
; a copy is saved at intervals for later output. The integration step length is  , and must be kept small to keep the integration stable. (It has been optimized to avoid instability when demonstrating the longest integrations.)
, and must be kept small to keep the integration stable. (It has been optimized to avoid instability when demonstrating the longest integrations.)
This leads to the expressions  that are built into the function Euler5. It should be noted that the two related equations are the result of changing the parametric multipliers within the functionals
that are built into the function Euler5. It should be noted that the two related equations are the result of changing the parametric multipliers within the functionals  and
and  , and not in their derivatives. Changing a multiplier for either
, and not in their derivatives. Changing a multiplier for either  or
or  would completely alter the results.
would completely alter the results.
For more information, see the related web pages on the soliton, Euler model, compacton, and wavelet.
Permanent Citation