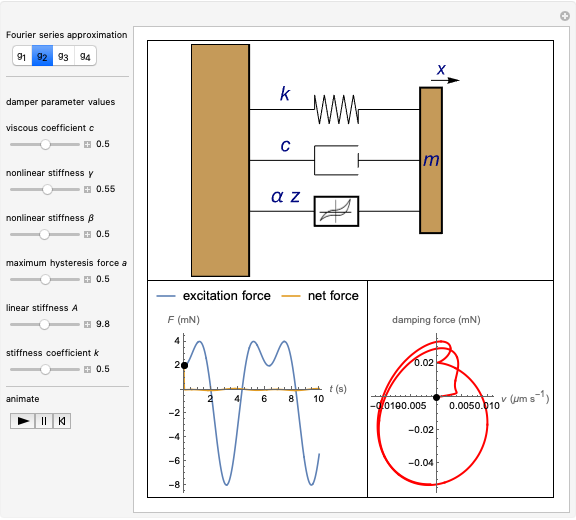
Bouc-Wen Model: Magnetorheological Fluid Damping for Micro-Vibration Control

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
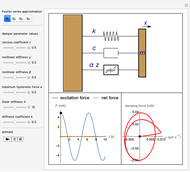
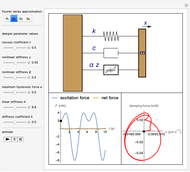
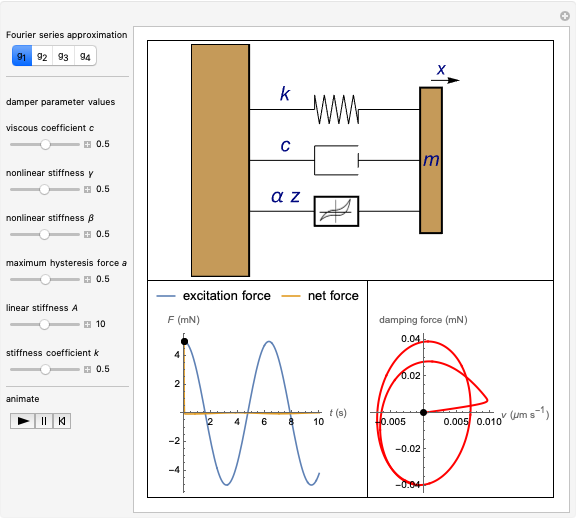
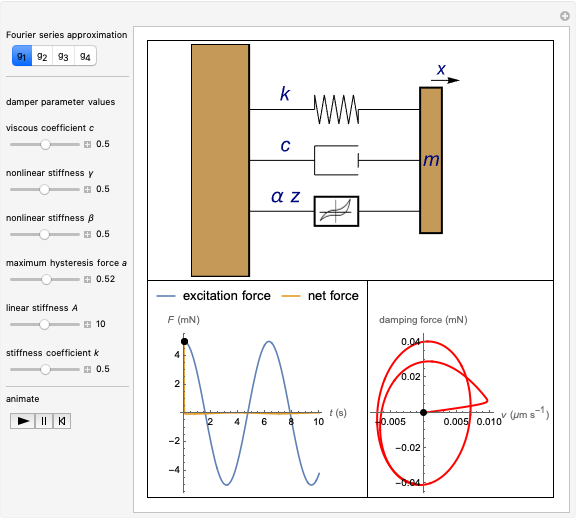
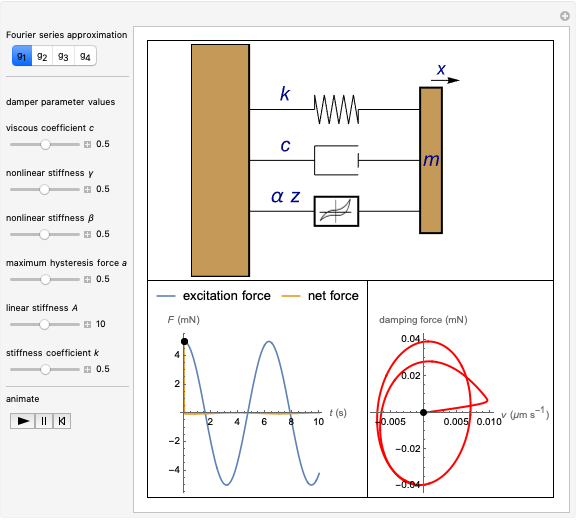
This Demonstration simulates a magnetorheological (MR) fluid damper that lets you explore the mitigation of micro-vibrations. The viscosity of an MR fluid depends on the external magnetic field, a property that makes it very useful for damping applications. The Bouc–Wen model is applied to the analysis of such systems (see Details). The top figure shows an animated Bouc–Wen model; bottom-left shows the excitation force function and the net force function (after the excitation force has been dampened); bottom-right shows the hysteresis curve that describes the MR damping.
Contributed by: Mohnish Raghu (Pioneer Academics) (August 2022)
Advised by: Z.J. Kabala (Duke University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In recent years, the demand for new "smart materials" has been increasing. This has stimulated research on magnetorheological (MR) fluids. MR fluids contain small magnetic particles, with diameters ranging from 0.01 to 20 µm, disbursed in an organic base fluid [1]. Normally, these particles are distributed randomly within the fluid, with the viscosity approximating that of the base fluid. However, in an external magnetic field, the particles align themselves in chains along the lines of magnetic flux. This greatly increases the viscosity of the fluid, now approaching that of a viscoelastic solid. This property renders them very useful as shock absorbers, vibration dampers and prop shaft mounts. A limited amount of research and modeling has been conducted on the damping of micro-vibrations—a phenomenon that is important in the aerospace industry, with many spacecraft and space stations experiencing micro-vibrations that can disrupt and damage vibration-sensitive equipment, in addition to affecting optical communications payloads [2]. This problem of micro-vibrations is made even more challenging when the constraints of a lightweight, compact and energy-efficient damper are considered [2]. MR dampers are potentially effective in solving this problem. This Demonstration focuses on numerical modeling of an MR damper applied to the mitigation of micro-vibrations.
When an MR fluid is exposed to an external magnetic field, the domains align themselves along the field, thus increasing the fluid's viscosity. However, when the external magnetic field is removed, MR fluids retain some of their magnetism, along with the effects on viscosity, a phenomenon known as hysteresis. When considering damping applications, this hysteresis behavior becomes essential for the action of the damper, particularly for control of micro-vibrations.
The Bouc–Wen model is a parametric dynamic model that integrates the hysteresis behavior and is thus invaluable for modeling these dampers. The Bouc–Wen model has been described as "semi-empirical," as it uses the theory of hysteresis, augmented by "black-box" modeling, by adjusting the parameters for each application [3]. Its potential applicability in the field of micro-vibrations was further considered by A. Rossi et al. [4]. MR dampers are controlled by electromagnets, and thus an underlying assumption of this model is that the voltage that controls the magnetic field in the electromagnet is directly proportional to the velocity  of the excitation. This is why the hysteresis curves produced by this model are plotted as force-velocity graphs.
of the excitation. This is why the hysteresis curves produced by this model are plotted as force-velocity graphs.
From the Bouc–Wen model—illustrated in the bottom-left figure—the following equation for the damper can be derived [4, Eqn. 7]:

where  is the mass of the oscillator,
is the mass of the oscillator,  is the excitation force (micro-vibration),
is the excitation force (micro-vibration),  is the viscous coefficient,
is the viscous coefficient,  is the stiffness coefficient,
is the stiffness coefficient,  is the displacement of vibration,
is the displacement of vibration,  is the maximum hysteresis force, and
is the maximum hysteresis force, and  is an evolutionary variable of the Bouc–Wen block defined by the following equation [4, Eqn. 8]:
is an evolutionary variable of the Bouc–Wen block defined by the following equation [4, Eqn. 8]:
 ,
,
where  is the linear stiffness of the hysteresis part,
is the linear stiffness of the hysteresis part,  and
and  are the nonlinear stiffness and damping character, and
are the nonlinear stiffness and damping character, and  is the smoothness of the system [5].
is the smoothness of the system [5].
This Demonstration explores a specific application of MR dampers (dampening micro-vibrations) with the parameters  ,
,  for an MR damper, and
for an MR damper, and  (micro-vibration) is defined by Fourier cosine series
(micro-vibration) is defined by Fourier cosine series  , where
, where  ,
,  ,
,  , and
, and  .
.
The motions depicted in the animated Bouc–Wen model (top figure) are magnified for better visibility.
This Demonstration was inspired by and uses results from several publications and from other Wolfram Demonstrations, as listed in the References.
References
[1] S. Genc, "Experimental Studies on Magnetorheological Fluids," Encyclopedia of Smart Materials (A.-G. Olabi, ed.), Oxford: Elsevier, 2022 pp. 248–259. doi:10.1016/B978-0-12-803581-8.12095-8.
[2] C. Dennehy and O. S. Alvarez-Salazar, "Spacecraft Micro-Vibration: A Survey of Problems, Experiences, Potential Solutions, and Some Lessons Learned," NASA/TM-2018-220075. ntrs.nasa.gov/search.jsp?R=20180006315.
[3] M. Ismail, F. Ikhouane and J. Rodellar, "The Hysteresis Bouc–Wen Model: A Survey," Archives of Computational Methods in Engineering, 16(2), 2009 pp. 161–188. doi:10.1007/s11831-009-9031-8.
[4] A. Rossi, F. Orsini, A. Scorza, F. Botta, N. Pio Belfiore and S. Andrea Sciuto, "A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods," Actuators, 7(2), 2018 16. doi:10.3390/act7020016.
[5] H. Gao, L. Jézéquel, E. Cabrol and B. Vitry, "Characterization of a Bouc–Wen Model-based Damper Model for Automobile Comfort Simulation," Surveillance, Vishno and AVE Conferences, INSA-Lyon, Université de Lyon, Jul 2019, Lyon, France. hal.archives-ouvertes.fr/hal-02188563.
[6] A. E. Charalampakis. "Single-Degree-of-Freedom Bouc–Wen Model with Mathematica (Sinusoidal Excitation)." (Feb 2, 2022) www.charalampakis.com/research/mathematica-notebooks/single-degree-of-freedom-bouc-wen-model-with-mathematica-sinusoidal-excitation.
[7] S. Wilkerson. "Mass Oscillating between a Spring and a Damper" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/MassOscillatingBetweenASpringAndADamper.
Permanent Citation