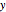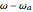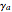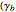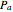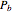Cavity Quantum Electrodynamics with Bosons: Emission Spectra in the Strong and Weak Coupling Regimes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
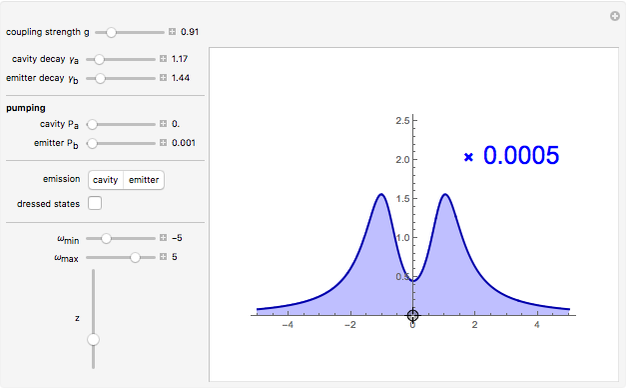
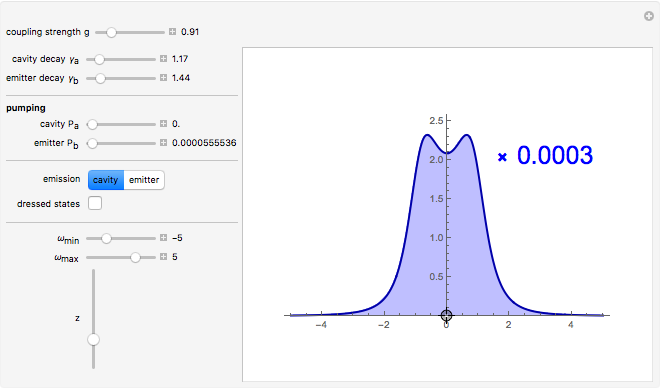
Placing an optical emitter—like an excited atom—in a cavity alters its emission properties. Its decay can thus be enhanced (returning to its ground state more rapidly) or inhibited (staying in the excited state for a longer time). This manifests in the optical emission as a broadening or narrowing of the lineshape, respectively (a δ line in a spectrum corresponds to a system with infinite lifetime). When the coupling of the emitter to the cavity becomes large enough, the probability of reabsorbing its emitted photon becomes important, and a sequence of emissions and absorptions can take place. This regime is non-perturbative, and instead of a mere renormalization of the lifetime, a new quantum regime is reached where the atom and the photon vanish to give rise to new quantum states, known as dressed states (in the atomic community) or polariton states (in the solid-state community). The optical emission of these systems is a spectral doublet, known as the Rabi doublet after the Rabi oscillations of the excitation between the atom and the cavity.
[more]
Contributed by: Fabrice P. Laussy and Elena del Valle (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
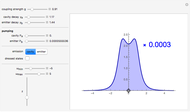
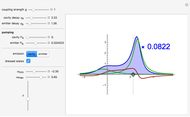
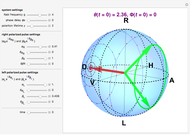
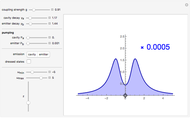
The spectrum of emission is computed from the Wiener-Khintchine theorem for the steady state of the coupled light-matter system established under the interplay of their decay and incoherent pumping. The case of spontaneous emission, which is more specific to the atomic case (rather than emission of a steady state, which is more typical in the semiconductor case), is recovered when pumping rates are vanishingly small: any one of the pumping rates can be set to zero, in which case the other one is forced to assume a very small but nonzero value (otherwise there would be no emission). When the pumping is non-vanishing, renormalization of the lines due to Bose stimulation is observed. The spectra are normalized to unity for clarity. Their actual normalization is provided as a multiplicative factor in inset. A rough estimate of an upper bound of the pumping is made to ensure that sliders do not allow pumping the system too much and having populations diverge. However, at nonzero detunings in particular, this would be unnecessarily restrictive to assume, therefore the warning "The system has diverged" is issued if the configuration leads to an infinite accumulation of particles (we are dealing with bosons). Simply lower the pumping rates to recover a steady state.
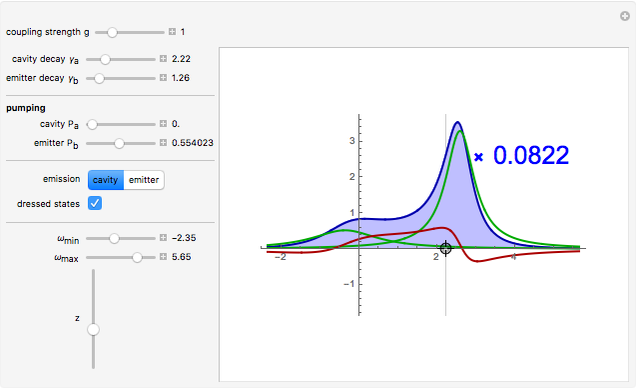
The qualitative physics of strong-coupling of light and matter in the linear regime or, equivalently, with bosons, is very simple: a Rabi doublet is produced at resonance. The emitter and photon lines anticross when the emitter energy spans over the cavity (that sits at zero). One can observe this phenomenon neatly in this Demonstration by dragging the emitter and seeing the "level repulsion" when it is brought in resonance with the cavity. Depending on the parameters and the channel of detection (cavity or direct emission of the emitter), the anticrossing is more or less clear and can assume a surprisingly wide variety of shapes. When broadening is large, the possibility of tracing two peaks can be lost, giving rise to an apparent crossing of the lines, but anticrossing is recovered if one follows the decomposition into dressed states that exhibit a clear level repulsion, although this is not apparent in the total emission spectrum. Another interesting fundamental feature of light-matter interaction to investigate through this Demonstration is the loss of strong-coupling. Ticking the "dressed states" box and, at resonance, lowering the coupling strength  until the spectrum becomes red (indicating it is now in weak coupling), one can see how the two split dressed states collapse into each other and a degenerate emission at the origin takes over. The smooth transition in the total spectrum results from a strong qualitative change in the underlying nature of the modes. In some particular cases (e.g.,
until the spectrum becomes red (indicating it is now in weak coupling), one can see how the two split dressed states collapse into each other and a degenerate emission at the origin takes over. The smooth transition in the total spectrum results from a strong qualitative change in the underlying nature of the modes. In some particular cases (e.g., 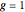 ,
, 
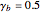 ,
,  , and
, and  ) one can see that even in weak coupling, there can be two peaks at resonance (because of some interference rather than because of dressed states splitting). Therefore, although the basic qualitative effect is very simple—a Rabi doublet—many surprising or counterintuitive features can arise from this most simple case of quantum light-matter interaction. In particular, a doublet in a luminescence spectrum is not an assurance of strong coupling.
) one can see that even in weak coupling, there can be two peaks at resonance (because of some interference rather than because of dressed states splitting). Therefore, although the basic qualitative effect is very simple—a Rabi doublet—many surprising or counterintuitive features can arise from this most simple case of quantum light-matter interaction. In particular, a doublet in a luminescence spectrum is not an assurance of strong coupling.
Most results of this Demonstration follow from F. P. Laussy et al., "Strong Coupling of Quantum Dots in Microcavities," Phys. Rev. Lett., 101, 2008 083601 and F. P. Laussy et al., "Luminescence Spectra of Quantum Dots in Microcavities. I. Bosons," arXiv:0807.3194.
Good introductions to cQED can be found in S. Haroche and D. Kleppner, "Cavity Quantum Electrodynamics," Phys. Today, 42(1), 1989 pp. 24–30 for atoms, and in G. Khitrova et al., "Vacuum Rabi Splitting in Semiconductors," Nature Phys., 2, 2006 pp. 81–90 for semiconductor microcavities.
Snapshot 1: typical lineshape of the spontaneous emission of an atom placed in a macroscopic cavity
Snapshot 2: corresponding emission of a quantum dot exciton in a semiconductor microcavity
Snapshot 3: a general case with detuning and decomposition of the total spectrum (blue) into Lorentzian emission of the dressed states of light and matter, and a dispersive correction due to their coupling
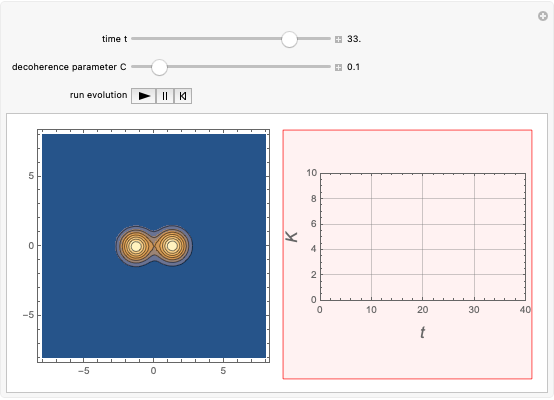
Snapshot 4: Bose-Einstein condensation in the very strong coupling regime: note the very large number of particles
Snapshot 5: weak coupling
Permanent Citation