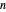Circle of Lamps

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
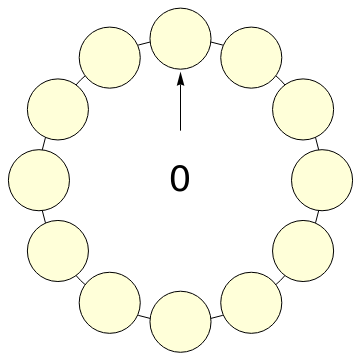
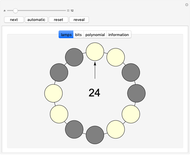
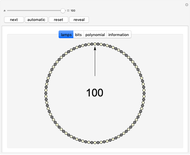
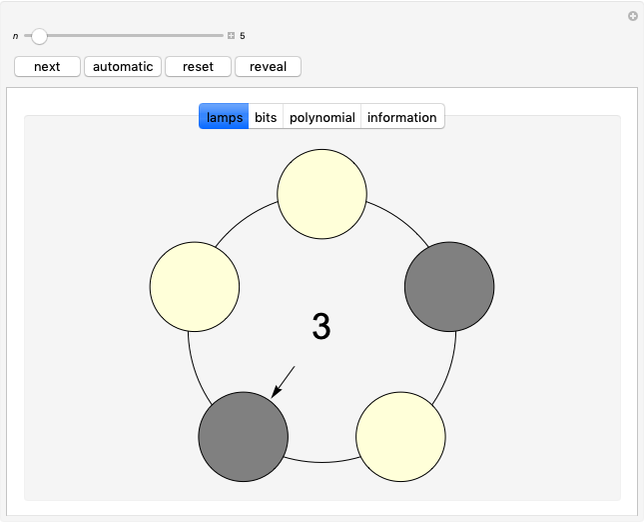
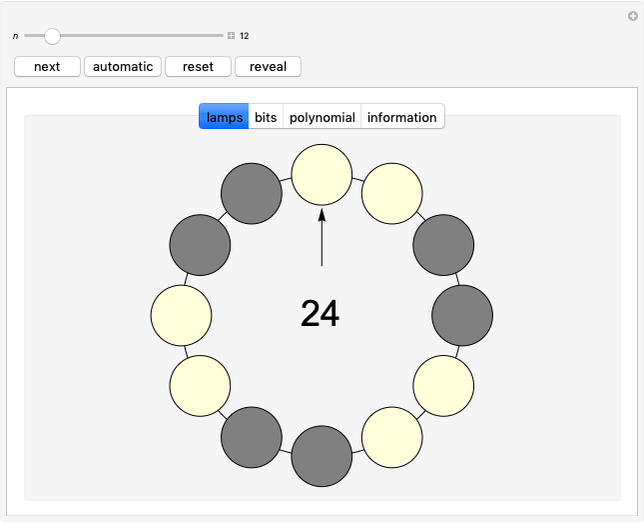
In a circle of 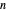 lamps, initially all the lamps are on. Go clockwise around the circle, examine each lamp, and change the state of the next lamp according to the following rule. If the lamp being examined is on, then the next lamp's state is flipped (switch the lamp from on to off, or vice versa). If the lamp being examined is off, then the next lamp remains as it was. The number in the middle is the step number.
lamps, initially all the lamps are on. Go clockwise around the circle, examine each lamp, and change the state of the next lamp according to the following rule. If the lamp being examined is on, then the next lamp's state is flipped (switch the lamp from on to off, or vice versa). If the lamp being examined is off, then the next lamp remains as it was. The number in the middle is the step number.
Contributed by: Tom Verhoeff (July 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration was inspired by Problem 6 from [1].
The arrow points to the currently examined lamp. The "next" button steps to the next state. The "automatic" button steps automatically until returning to the current state or the all-on state (whichever comes first). The "reset" button switches all lamps on and examines the lamp at the top. Click the "reveal" button to change it into a button that serves as a hint for answering the first question. You can also change the state of each lamp by clicking it. The step counter can be reset to zero by clicking it.
To answer the second question, the problem can be modeled as a linear feedback shift register or a cellular automaton, with 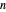 binary flip-flops/cells; also as a polynomial over GF(2) (the binary field), that is, a polynomial with binary coefficients of degree
binary flip-flops/cells; also as a polynomial over GF(2) (the binary field), that is, a polynomial with binary coefficients of degree 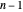 where the next state is obtained by multiplying the polynomial by
where the next state is obtained by multiplying the polynomial by 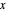 and taking the result modulo
and taking the result modulo 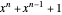 (the so-called characteristic polynomial of this update process; it has degree
(the so-called characteristic polynomial of this update process; it has degree 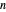 ).
).
For more information on polynomials over finite fields and linear feedback shift registers, see [2].
The theory tells us that because the characteristic polynomial does not vanish for  , each state belongs to a unique cycle, because each state has a unique preceding state. The cycle with the longest period is the one with the state 1, and this state evolves into the all-on state. That longest period is equal to the so-called polynomial order of the characteristic polynomial, which is the smallest positive exponent
, each state belongs to a unique cycle, because each state has a unique preceding state. The cycle with the longest period is the one with the state 1, and this state evolves into the all-on state. That longest period is equal to the so-called polynomial order of the characteristic polynomial, which is the smallest positive exponent  such that
such that  equals 1 modulo the characteristic polynomial. This number can be calculated (see the "information" button). Other cycles have a period that is a divisor of this longest period. In case the characteristic polynomial is primitive, the longest period equals
equals 1 modulo the characteristic polynomial. This number can be calculated (see the "information" button). Other cycles have a period that is a divisor of this longest period. In case the characteristic polynomial is primitive, the longest period equals  . Note that 0 (all off) always forms a cycle of length 1 on its own.
. Note that 0 (all off) always forms a cycle of length 1 on its own.
For example, in the case of 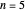 , we have that the characteristic polynomial
, we have that the characteristic polynomial  factors as
factors as 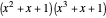 , where both factors are primitive, having longest periods 3 and 7, respectively. Therefore, the period for
, where both factors are primitive, having longest periods 3 and 7, respectively. Therefore, the period for 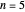 equals
equals  . There are also three other cycles: containing
. There are also three other cycles: containing 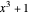 (period 7),
(period 7), 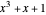 (period 3), and 0 (period 1).
(period 3), and 0 (period 1).
Warning: the computation of the polynomial order takes a while for 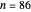 and
and 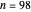 .
.
References
[1] International Mathematical Olympiad. "34th IMO 1993." imo-official.org/year_info.aspx?year=1993.
[2] R. Lidl and H. Niederreiter, Chapters 3 and 6, Introduction to Finite Fields and Their Applications, New York: Cambridge University Press, 1994.
Permanent Citation