Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Comparing Loxodromes and Great Circle Routes

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

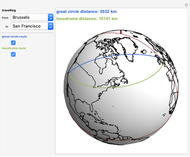
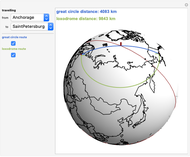
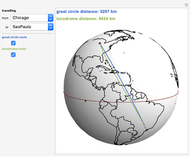
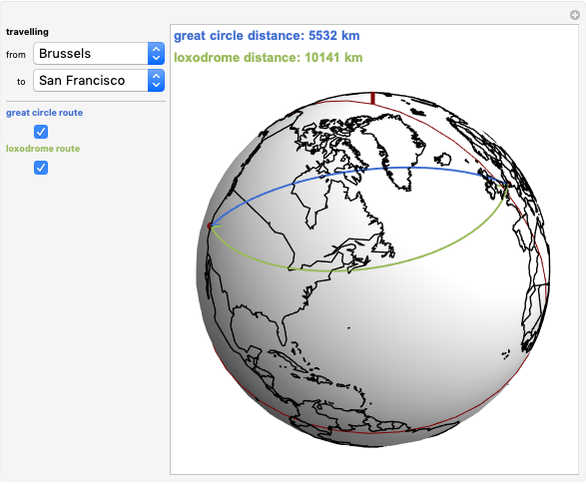
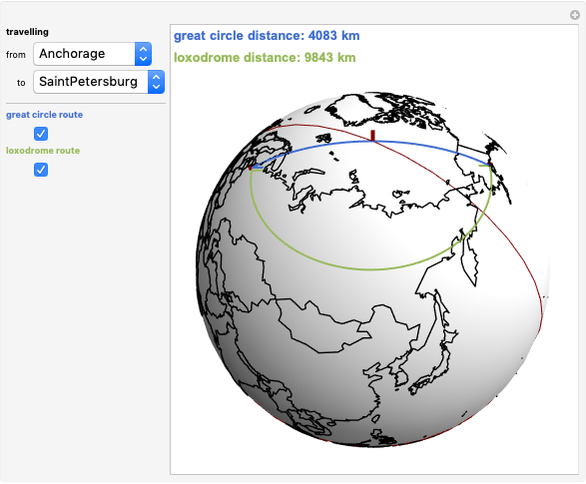
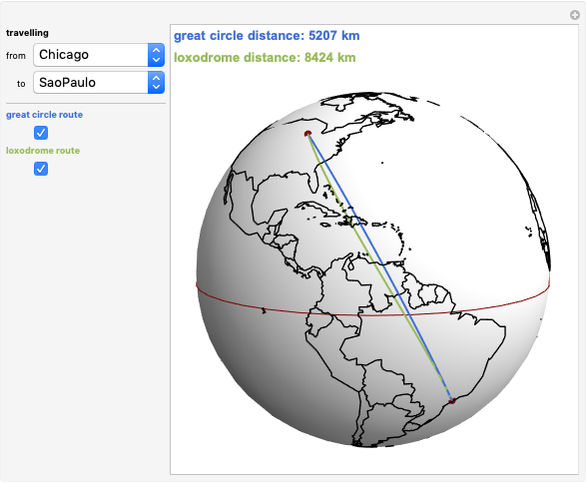
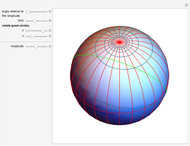
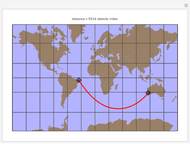
This Demonstration plots both the great circle route and the shortest loxodrome route between selected cities on the globe. A great circle on a sphere cuts the sphere into two congruent halves. A loxodrome, also known as a rhumb line, is a path on a sphere that cuts all meridians at the same angle (not 90°)

[more]

Although historically loxodromes were widely used for navigation, the loxodrome route is not the shortest one. The shortest route is the great circle route, as used in modern air traffic and navigation..

[less]

Contributed by: Erik Mahieu (March 2010)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The loxodrome equations used were derived from the article by J. Alexander, "Loxodromes: A Rhumb Way to Go," College Mathematics Journal, 77(5), 2004 pp. 349–356.

From the snapshots you can see that the difference between the routes is greatest on East-West routes or routes close to the poles. The difference gets smaller on North-South routes or routes closer to the equator.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send