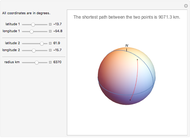
Shortest Path between Two Points on a Sphere

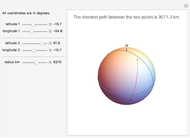
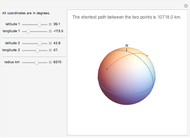
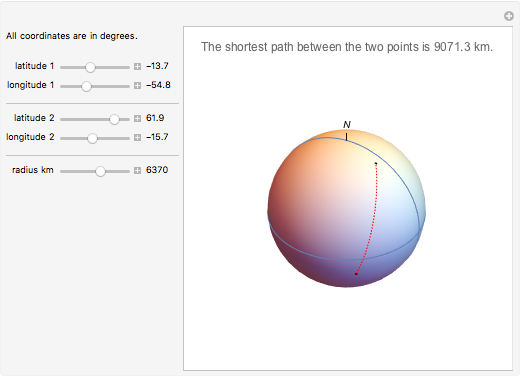
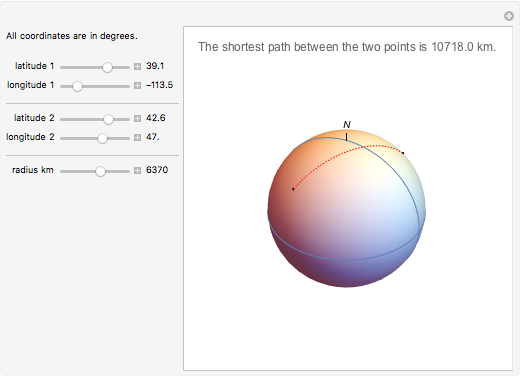
The shortest path between two points on the surface of a sphere is an arc of a great circle (great circle distance or orthodrome). On the Earth, meridians and the equator are great circles. Between any two points on a sphere that are not directly opposite each other, there is a unique great circle. The two points separate the great circle into two arcs and the length of the shorter arc is the shortest path between the two points. Points are given by their latitude and longitude.