Distortions in Map Projections

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
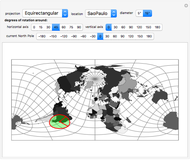
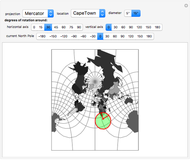
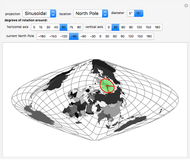
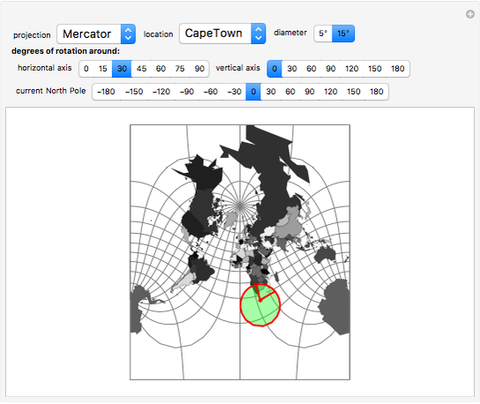
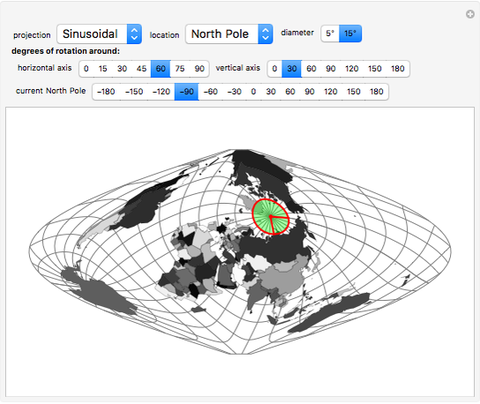
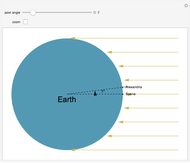
All map projections give rise to certain distortions. This Demonstration shows these distortions for different projections by applying three sequential rotations to the globe: the first is about the  axis, the second is about the
axis, the second is about the  axis, and the third is about the North Pole after the first two rotations.
axis, and the third is about the North Pole after the first two rotations.
Contributed by: Erik Mahieu (March 2011)
Parametric equations suggested by: Arnold Debosscher
Open content licensed under CC BY-NC-SA
Snapshots
Details
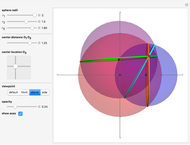
The parametric equations for the geographic coordinates of a spherical circle were derived by applying the Mathematica function TransformationFunction: RotationTransform[{{0, 0, 1}, {Cos[λ] Cos[ϕ], Sin[λ] Cos[ϕ], Sin[ϕ]}}] to a circle parallel to the 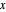 -
-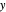 plane:
plane:  .
.
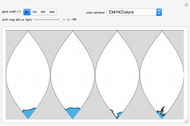
For clarity, a circle corresponding to a solid angle of 2×5° or 2×15° is used for the Tissot indicatrix. The grid on the world map is spaced at 15° in both directions.
In conformal projections (Mercator, stereographic), where angles are preserved around every location, the Tissot indicatrix is always a circle, with varying size.
In equal-area projections (Albers, Lambert cylindrical, sinusoidal), where area proportions between objects are conserved, the Tissot indicatrix has the same area, although its shape and orientation vary with location.
The properties of the Tissot indicatrix are for an infinitesimally small circle and hence more apparent for a 5° diameter than for a 15° diameter.
To better demonstrate angular distortion, two radii, pointing east and north, are added to the indicatrix.
A pure function representing stereographic projection (from the North Pole to the plane  ) has been added to the standard WorldPlot Package projections.
) has been added to the standard WorldPlot Package projections.
See also:
Permanent Citation