Complex Polynomials

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
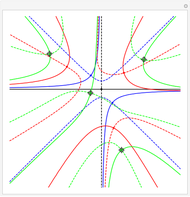
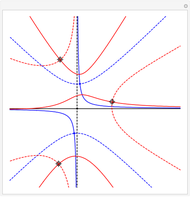
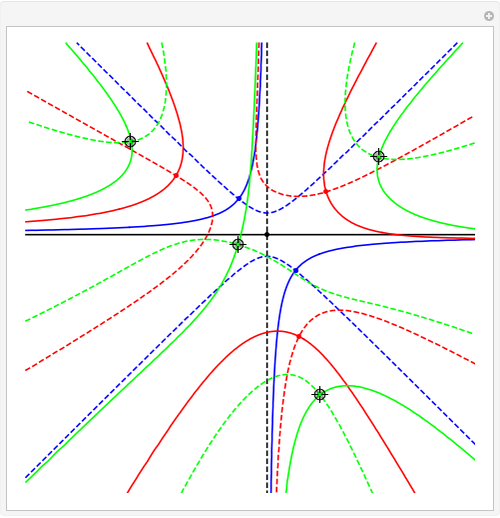
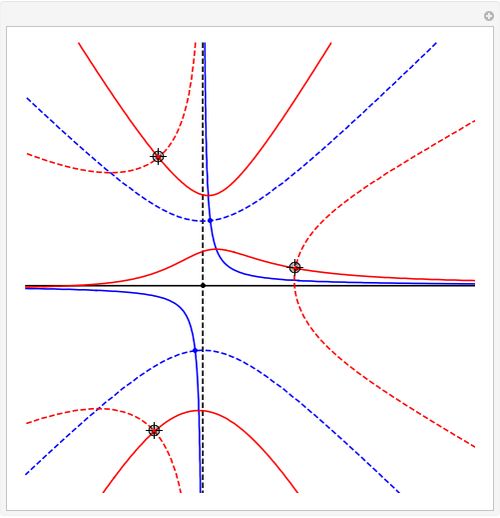
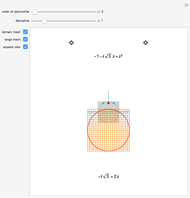
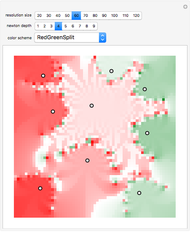
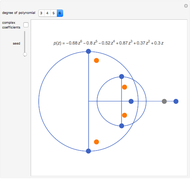
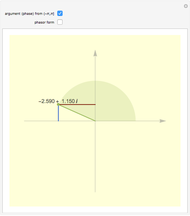
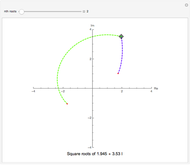
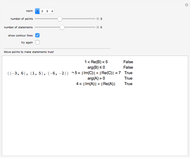
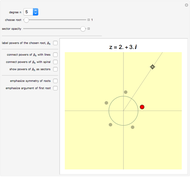
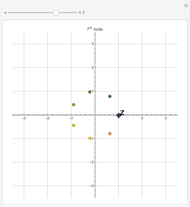
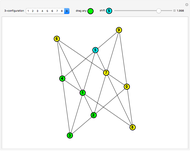
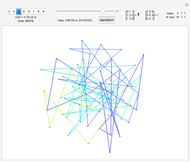
Four points in the complex plane can be the roots of a complex polynomial of degree four. Solid lines indicate where the real part is zero and dashed lines indicate where the imaginary part is zero. These lines intersect at the chosen roots. The successive derivatives of the complex polynomial behave similarly. Complex points can be added or removed with Alt+Click. Hover over a point to see its value. Notice that derivative roots all lie within the convex hull of the original roots, due to the Lucas–Gauss theorem (linked below).
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Complex Polynomials"
http://demonstrations.wolfram.com/ComplexPolynomials/
Wolfram Demonstrations Project
Published: March 7 2011